| précédent | sommaire | suivant |

Les armes à distance dans les jeux de rôle — 1

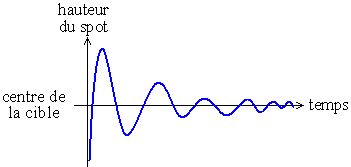
Considérons une personne munie d'un fusil. Le fusil dispose d'un laser insivible qui permet de savoir la partie de la cible qui est visée. Si l'on enregistre la position du spot par rapport au centre de la cible, on verra probablement des oscillations s'amortissant :

• au départ, la personne épaule, le spot monte et se positionne approximativement, sans doute assez loin du centre ;
• la personne vise le centre, mais il lui faut probablement plusieurs mouvements pour l'avoir bien en joue ;
• une fois le centre visé, le spot continue à osciller  : personne n'étant capable de rester totalement immobile, il faut corriger en permanence la position.

Fig. 1 - Stabilisation de la position du fusil lors de la visée : représentation de la hauteur du spot par rapport au centre de la cible en fonction du temps

Imaginons que la hausse soit mal réglée. La visée sera alors systématiquement plus haute ou plus basse que le centre. Un tel écart systématique peut aussi survenir si le tireur doit compenser un effet et le fait mal, par exemple le fait qu'avec un arc, il faille viser plus haut que le centre, et ce d'autant plus que la cible est loin.

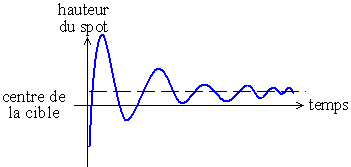
Fig. 2 - Écart de visée

Si la personne reste trop longtemps en joue, on peut s'attendre à ce qu'elle fatigue et se déconcentre, et donc à voir l'amplitude des oscillations augmenter et leur position moyenne dévier.

Il y a donc typiquement deux type d'erreurs, que l'on rencontre d'ailleurs dans tous les domaines :

• la dispersion : lorsqu'une personne effectue plusieurs tirs successifs, les tirs ne sont pas exactement au même endroit, ils sont dispersés ;
• l'erreur de visée : lorsqu'une personne effectue plusieurs tirs successifs, la position moyenne des tirs est décalé du centre de la cible.

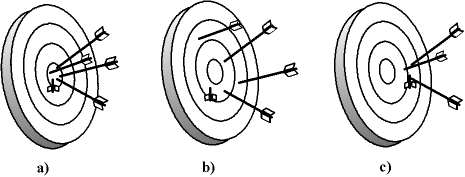
Fig. 3 - Dispersion et erreur de visée
a) Faible dispersion, pas d'erreur de visée
b) Grande dispersion, pas d'erreur de visée
c) Faible dispersion, erreur de visée

La dispersion dépend de :

• la stabilité du tireur, sa capacité à maîtriser ses mouvements, à garder son calme et sa concentration (ce sont les « oscillations résiduelles ») ;
• la précision de l'arme, sa qualité, la stabilité du projectile ;
• l'appui : arme de poing bras tendu, arme épaulée, arme sur pied ;
• la stabilité des conditions : vent constant, sol stable…

• des conditions : par exemple vent déviant les projectiles ;
• du réglage de l'arme, du viseur ;
• de l'expérience du tireur, de sa capacité à corriger les écarts, ainsi que du temps passé à viser et éventuellement des tirs précédents qui ont pu servir à ajuster.

On modélise traditionnellement la dispersion par une loi statistique du type loi de Gauss (ou loi normale)¹, semblable à une courbe en cloche : la courbe ci-dessous repréte la probabilité que le projectile atteigne un point en fonction de la distance entre le points visé.

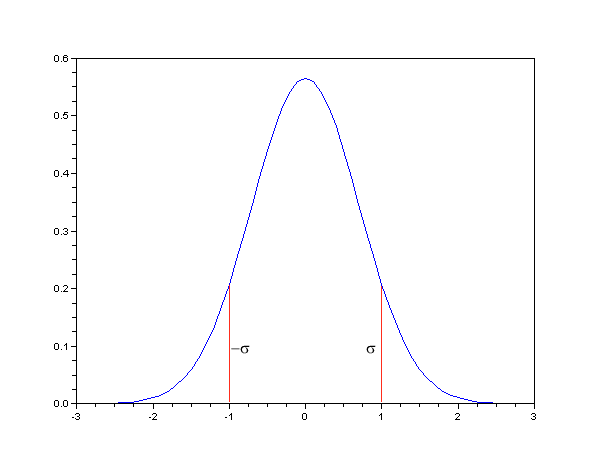
Fig. 4 - Loi de Gauss 1/√π·exp(-x²) et écart type σ

On peut représenter la probabilité en fonction de la position par rapport au point visé (on peut s'écarter du point central dans toutes les directions). La figure ci-dessous représente cette probabilité sous la forme d'une surface 3D (la hauteur de la surface représente la probabilité) et sous la forme d'une carte de couleur (plus la couleur est foncée, plus la probabilité est grande).

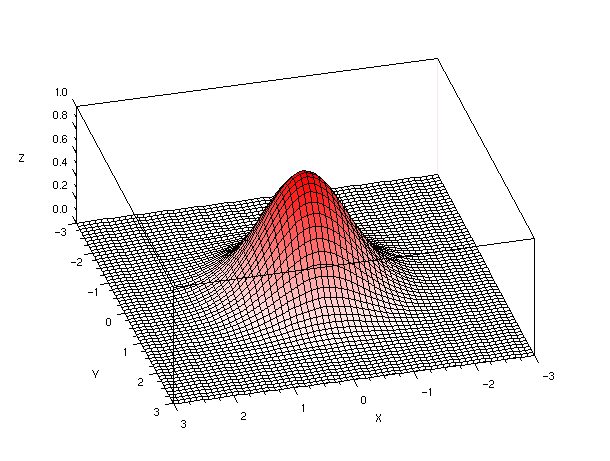
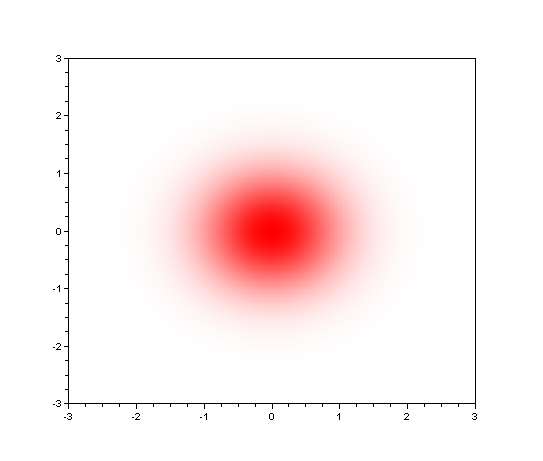
Fig. 5 - Probabilité selon la position

La largeur de la dispersion est en général donnée par l'écart type σ (en anglais : standard deviation). Si l'on considère une cible ayant le rayon de l'écart type, avec une loi gaussienne, environ 67 % des tirs seront dans la cible. La direction de déviation est par contre a priori totalement aléatoire (sauf si l'on bloque une direction).

On peut estimer en première approximation que l'écart type est proportionnel à la distance. Cela revient à considérer que l'on a un cône de dispersion. Plus on est loin, et plus la dispersion sera grande. Si l'on appelle « disque d'impact » le disque dans lequel tombent tous les tirs, alors le rayon de ce disque est proportionnel à la distance, et vaut trois fois l'écart type (ce 3 est un coefficient classique en statistiques²). Ce disque d'impact a toujours la même taille apparente.

L'erreur de visée, elle, est proportionnelle à la distance et sa direction est constante : plus on est loin, et plus le tir sera décalé par rapport au centre de la cible.

| début |

Notes

• 1 - On peut aussi envisager d'utiliser d'autres lois plus simples, comme par exemple une loi en triangle. Si l'on considère une loi triangulaire, l'écart type représente les deux-tiers de la base, et environ 56 % des tirs seront dans la cible. — retour
• 2 - La surface sous la gaussienne entre -3σ et 3σ représente en fait 99,73 % de la surface totale sous la gaussienne ; dans l'absolu, il faudrait tout l'espace pour avoir 100 %, ce qui signifie que par accident très rare, on pourrait se tirer dans le pied tout en visant de face — retour

| début | précédent | sommaire | suivant |