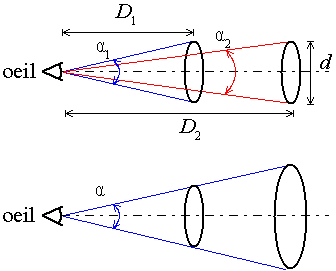
Fig. 6 - Distance et taille apparente
haut : plus l'objet est loin, plus l'angle avec lequel il est perçu est petit
bas : deux objets de taille différente peuvent être perçus avec la même taille apparente
| précédent | sommaire | suivant |
Supposons que l'on regarde un disque de diamètre d et situé à une distance D. Le disque réfléchit la lumière environnante, et certains de ces rayons réfléchis frappent notre œil, c'est ce qui fait que l'on voit l'objet. Les rayons réfléchis par l'objet et frappant notre œil forment un cône.
La taille perçue de l'objet est liée à l'angle α au sommet du cône. Ainsi, un petit disque vu de près aura la même taille qu'un grand disque vu de loin. Cette taille apparente constitue la première difficulté de visée.

Fig. 6 - Distance et taille apparente
haut : plus l'objet est loin,
plus l'angle avec lequel il est perçu est petit
bas : deux objets de taille différente peuvent être perçus
avec la même taille apparente
Notons que la visée se fait en faisant pivoter l'arme autour d'un point fixe, le tireur maîtrise donc l'angle de visée, pas à proprement parler la position sur la cible. Donc cette notion de cône, et de taille apparente, permet aussi de décrire la visée en elle-même.
La trigonométrie nous donne l'angle α en fonction du diamètre et de la distance :
tan α/2 = d / 2Dsoit
α = 2· arctan (d / 2D)On voit de ceci que ce qui importe, c'est le rapport entre le diamètre et la distance. Ainsi, si l'on prend deux disques dont le diamètre de l'un est le double de l'autre, ils auront la même taille apparente si le grand disque est deux fois plus loin que le petit.
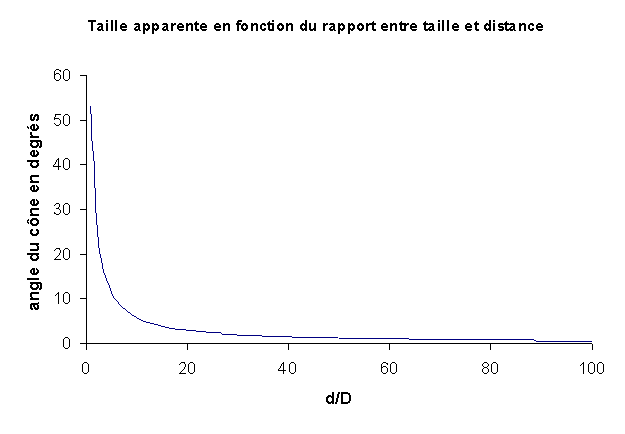
Fig. 7 - Taille apparente (angle du cône en degrés)
en fonction du rapport du diamètre sur la distance
Le graphique ci-dessus montre la taille apparente en fonction du rapport d / 2D. On constate que cette courbe est très proche d'une courbe en 1/x Si l'on prend comme distance de référence le diamètre du disque, alors pour une distance n fois plus grande, la taille apparente a été divisé par n. Ceci n'est pas très étonnant, la fonction tangente étant proche de la fonction identité (tan α ≈ α, en radians) aux faibles angles ; l'écart entre les deux fonctions est plus grand pour les grands angles, donc lorsque l'on se rapproche.
Nous avons ici considéré des disques. Ce qui importe en fait est l'angle solide auquel correspond l'objet, c'est-à-dire grosso modo le rapport entre la surface vue et la distance. Ceci peut permettre de comparer des objets de forme différente, mais la diminution de la taille apparente avec la distance garde la même forme, en 1/D. Par exemple, une personne de profil présente une surface valant à peu prè la surface présenté de profil, donc une taille apparente valant à peu près la moitié.
Le but d'un viseur est d'augmenter la taille apparente de la cible.
| début |