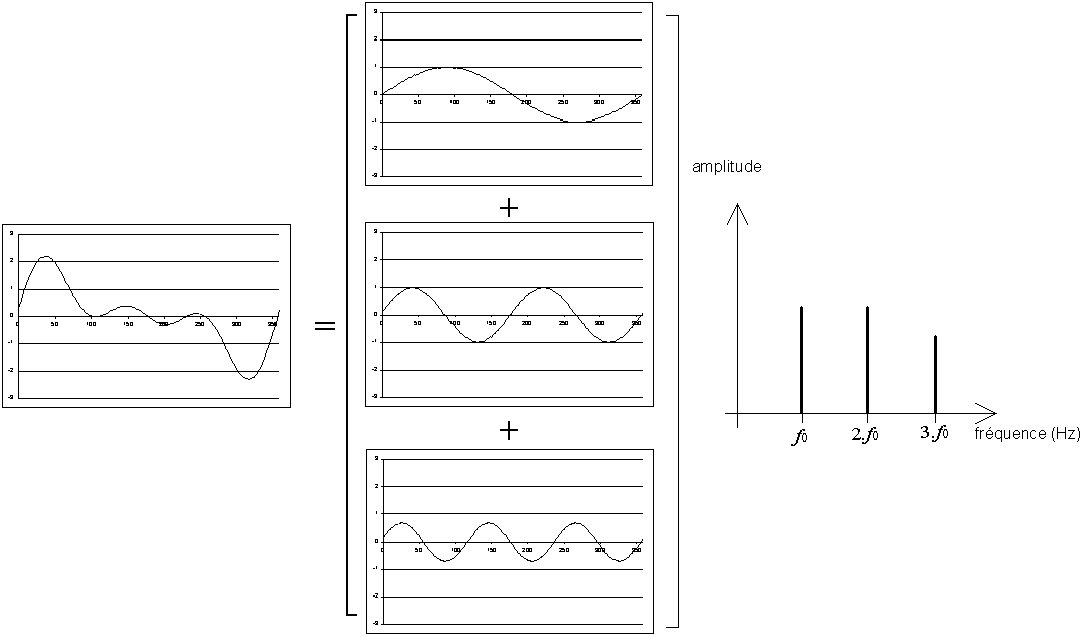
Fig. 1.1 - Décomposition en séries de Fourier
Cliquer ici pour un agrandissement
| précédent |
Une des manières de représenter une fonction de l'orientation de l'espace, est d'utiliser le développement en harmoniques sphériques. Le développement en harmoniques sphériques est l'équivalent, appliqué aux fonctions angulaires, du développement en séries de FOURIER1 pour les fonctions périodiques.

Fig. 1.1 - Décomposition en séries de Fourier
Cliquer ici pour un agrandissement
Les harmoniques sphériques sont utilisées en acoustique (reconstitution de l'effet d'espace par plusieurs haut-parleurs), en géophysique (représentation du globe terrestre, champ de gravitation, météorologie) et en physique quantique (développement d'une fonction d'onde, densité du nuage électronique), mais aussi dans tout domaine ou une valeur change en fonction de l'orientation (anisotropie), comme par exemple la distribution des orientations cristallines dans un solide (orientations préférentielles, texture). Ce dernier domaine fait même appels aux harmoniques sphériques généralisées, puisque l'orientation d'un cristal est décrite par trois angles au lieu de deux pour les autres domaines cités.
| début|
Plaçons-nous dans le plan (x,y), et considérons une fonction r=f(θ), r étant le rayon (la distance du point considéré à l'origine O), et θ l'angle entre le rayon et la droite Ox. Il s'agit là de coordonnées polaires habituelles.
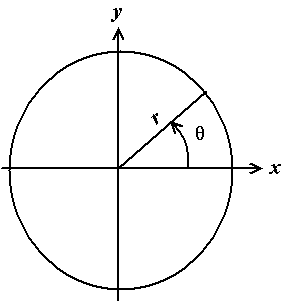
Fig. 1.2 - Repérage en coordonnées polaires dans le plan
Si nous déplions cette fonction, on peut la décomposer en série de Fourier. Si maintenant nous enroulons les fonctions sinusoïdales autour de O, nous voyons apparaître ce que nous pourrions appeler des "harmoniques circulaires".
Notre fonction ƒ peut donc se décomposer en harmoniques circulaires Yi(θ) :
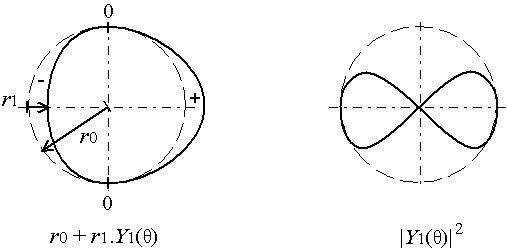
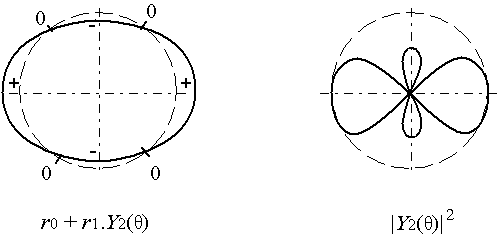
ƒ(θ) = ∑i = 0+∞ Ci.Yi(θ)Ci étant un coefficient réel. L'harmonique Y0 est fonction constante et correspond donc à un cercle, l'harmonique Yi correspond à une figure invariante par une rotation d'1/(i+1)ème de tour autour de O ; on dit qu'elle admet une symétrie d'ordre i+1.
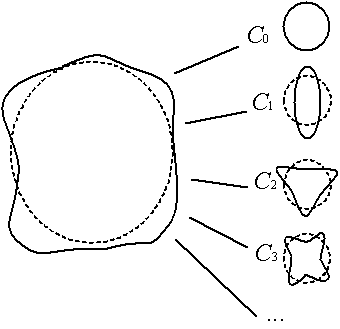
Fig. 1.3 - Décomposition d'une fonction angulaire
en une somme pondérée de fonctions élémentaires
Notes :
| début|
En fait, on n'utilise pas simplement des fonctions sin(n.ν.θ) et cos(n.ν.θ), comme dans les séries de FOURIER, mais les «polynômes de LEGENDRE2» Pl :
Yl(θ) = Pl(cos θ)avec
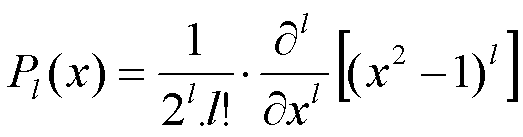
Les polynômes de LEGENDRE présentent l'avantage d'être des solutions de l'équation de LAPLACE3
Δ U = 0U étant une fonction de l'espace ; cette équation est particulièrement importante dans l'étude des potentiels (dont dérivent les champs physiques : champ électrique, champ magnétique, champ gravitationnel...). On obtient :
soit
∂U/∂x + ∂U/∂y + ∂U/∂z = 0
Notes :
| début|
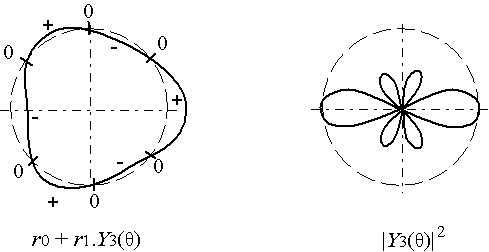
Nous représentons ces fonctions ci-après, sous trois formes :
| l = 1 | 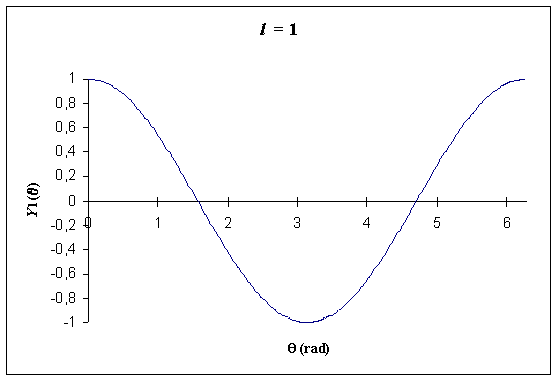 |
 |
| l = 2 | 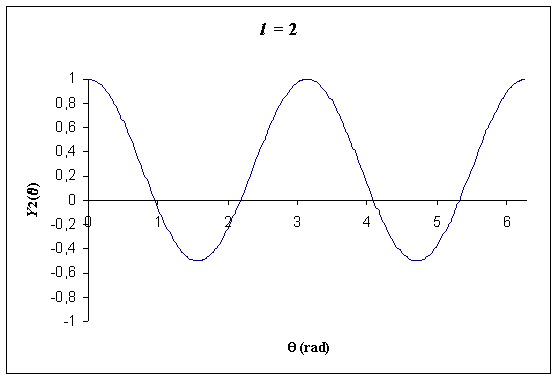 |
 |
| l = 3 | 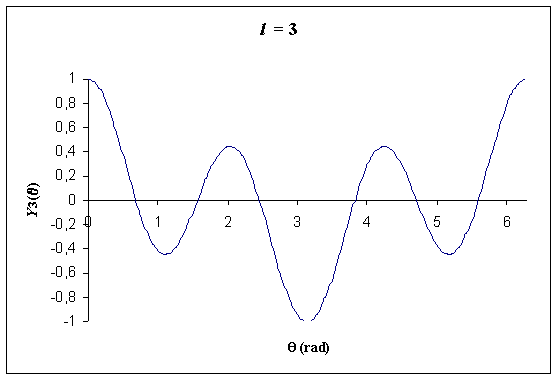 |
 |