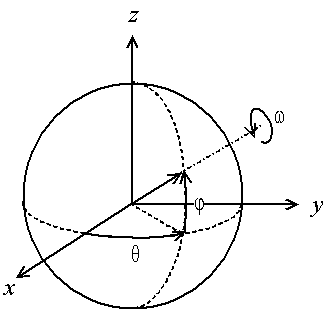
Fig. 3.1 - Repérage en coordonnées polaires dans l'espace
Considérons maintenant une fonction dépendant de trois angles, ƒ(θ, φ, ω).

Fig. 3.1 - Repérage en coordonnées polaires dans l'espace
Typiquement, cette fonction dépend de l'orientation qu'a un objet dans un référentiel. Pour décrire l'orientation de l'objet, on définit trois axes (e1, e2, e3) associés à l'objet. Initialement, ces axes sont alignés sur les axes (x, y, z) du référentiel ; puis, on fait tourner l'objet, les angles descriptifs θ, φ et ω sont les angles des rotations1. Un application typique est l'orientation des cristallites dans de la matière polycristalline (roche, métal), où l'on considère la fonction de distribution d'orientation (FDO, en anglais ODF - orientation distribution function), c'est à dire le volume de matière dans des cristaux dont l'orientation est dans un angle solide ([θ,θ+Δθ], [φ,φ+Δφ], [ω+Δω]).
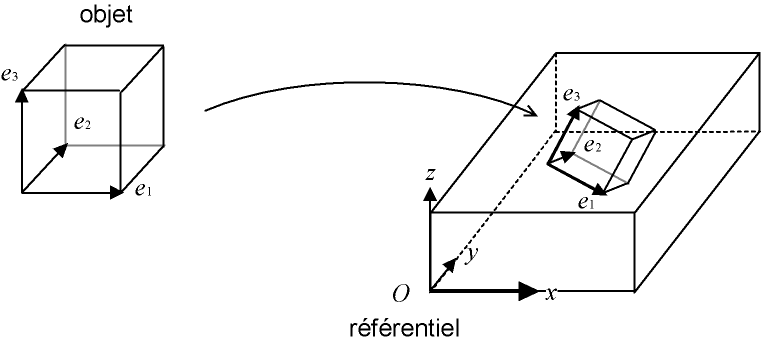
Fig. 3.2 - Orientation d'un objet dans un référentiel
Pour représenter cette orientation dans l'espace, on préfère souvent utiliser les angles d'EULER2 ; le repère (e1, e2, e3) lié à l'objet peut Ítre obtenu en appliquant trois rotations successives au repère (x, y, z) du référentiel :
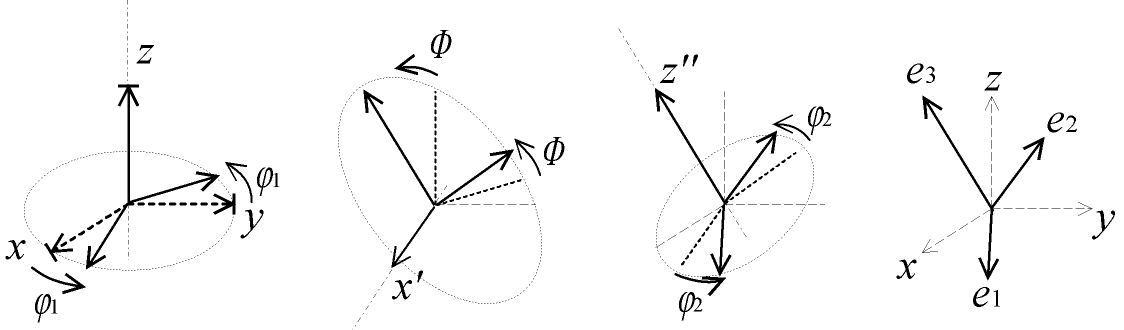
Fig. 3.2 - Orientation d'un objet et angles d'EULER
On peut donc considérer la fonction ƒ(φ1, Φ, φ2).
Notes :
| début |
De la mÍme manière que précédemment, cette fonction peut se décomposer en une série de fonctions élémentaires Tlm,n(φ1, Φ, φ2), l, m et n étant des paramètres entiers définissant la fonction :
ƒ(φ1, Φ, φ2) = ∑l=0+∞ ∑m=-ll ∑n=-ll Clm,n. Tlm,n(φ1, Φ, φ2)où Clm,n est une constante. Tlm,n(φ1, Φ, φ2) s'écrit :
Tlm,n(φ1, Φ, φ2) = eimφ2 . Plm,n(cos Φ) . eimφ1où Plm,n est la fonction associée de LEGENDRE généralisée :
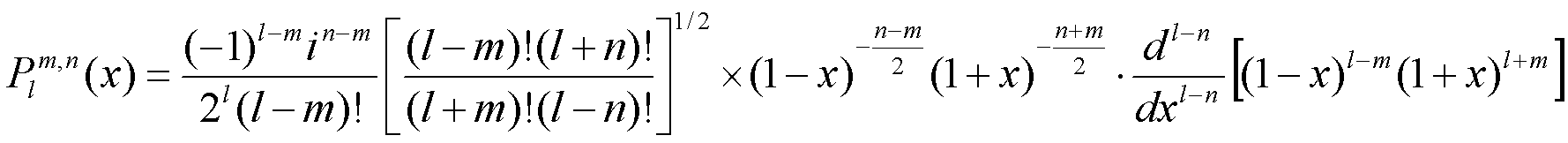
Quand x décrit [-1;1], cette fonction Plm,n(x) est soit réelle, soit imaginaire pure. T00,0(φ1, Φ, φ2) est la fonction isotrope (symétrie sphérique).