Fig. 2.1 - Montée du niveau de l'eau dans un verre
Remplissez un verre d'eau, mais pas complètement, et mettez doucement un petit objet dans le verre (par exemple, on l'accroche à un fil pour le descendre lentement), vous voyez que le niveau de l'eau monte.

Fig. 2.1 - Montée du niveau de l'eau dans un verre

Fig. 2.2 - Montée du niveau de l'eau dans une piscine
La vague est donc l'adaptation du milieu, en l'occurence le niveau d'eau, à la modification des conditions, en l'occurence l'arrivé d'un objet. Si la modification est lente par rapport à la taille de l'étendue d'eau, on a l'impression que l'eau monte de manière uniforme. Si par contre la modification est rapide par rapport à la taille de l'étendue d'eau, on voit apparaître une vague qui propage l'adaptation.
Il faut bien comparer ici la vitesse de la modification avec la taille du milieu. Si par exemple on jette l'objet dans le verre (étendue petite mais variation très rapide), on verra aussi apparaître des vagues.
On voit que la vague peut se caractériser par 4 paramètres :
NB : dans le cas des vagues de mer, celles-ci ne sont pas crées par la chute d'un objet, mais par le vent qui souffle à l'inverse du courant marin. Le phénomène est rendu complexe par le fait que, contrairement à la piscine, le fond n'est pas plan et le littoral pas droit, qu'il y a l'effet de marée, la variation des courants... Mais le fond du problème est le même : la mer s'adapte à des conditions changeantes (déplacements d'eau et d'air).
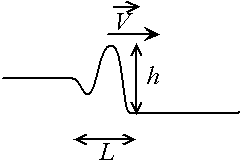
Fig. 2.3 - Paramètres pour décrire la vague
Dans le cas où le front est droit, la vague progresse en ligne droite, alors que dans le cas du front circulaire, la vague s'étend dans tous les sens. On considère souvent que l'on est en front droit ; en effet, d'une part, dans le cas du front circulaire, il suffit de voir qu'il y a une symétrie de révolution, d'autre part, lorsque l'on est loin du centre, le front paraît droit.
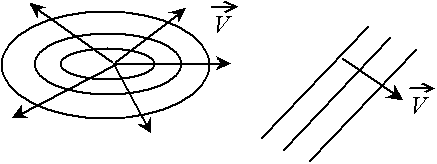
Fig. 2.4 - Forme de la vague, front circulaire et front droit
On voit que la vague est un objet qui se déplace ; pour l'étudier, il faut donc repérer sa position. Si l'on a un front droit, il suffit de prendre comme repère une droite perpendiculaire au front, cette droite montre donc la direction de propagation. On peut ensuite graduer cette droite (en mètre) à partir d'un point de référence, les graduation étant croissante dans le sens de propagation. On peut ainsi repérer un point sur cette droite par sa graduation (son abscisse) x.
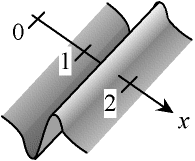
Fig. 2.5 - Repérage d'une vague
à l'aide d'une droite orientée et graduée
Avec la vague se déplace de l'énergie. Une vague très importante peut renverser une personne, faire chavirer un bateau, les vagues érodent une falaise et celle-ci s'effondre peu à peu. Mais un objet qui flotte reste toujours à la même position lors du passage de la vague, il monte et il descend, mais ne se déplace pas horizontalement : mettez du poivre dans un verre d'eau et faites une vague, le poivre ne bouge pas, le bouchon de la canne à pêche reste sur place lors du passage de la vague.
NB : les fortes vagues s'accompagnent souvent de courants marins puissant et de vents violents (tempête), qui, eux, peuvent faire dériver le bateau, mais ce ne sont pas les vagues qui le poussent (d'ailleurs, elles vont beaucoup plus vite). Le surfeur, quant à lui, ne se laisse pas porter par la vague, il glisse sur elle comme le skieur glisse sur la pente (et la pente de la montagne ne bouge pas...).
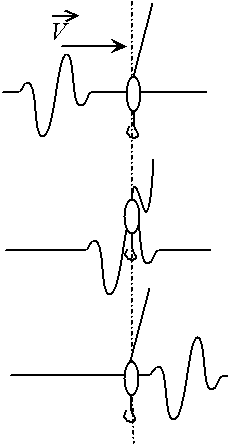
Fig. 2.6 - Le bouchon du pêcheur ne se déplace pas
après le passage de la vague
Donc, la vague est un déplacement d'énergie, pas de matière. L'énergie, c'est l'énergie potentielle de gravité, puisque l'eau est plus haute à l'endroit de la vague.
En fait, dans l'eau liquide, les molécules sont en constante agitation (mouvement Brownien), elles bougent dans tous les sens, mais il n'y a pas de déplacement en moyenne (une bouée dans de l'eau sans courant et sans vent ne bouge pas). Lors du passage de la vague, l'eau monte pour former la vague puis redescend ; ce n'est pas une montagne qui se déplace, à chaque endroit, c'est de l'eau "du coin" qui constitue la vague. Les molécules d'eau s'assemblent pour former un monticule, puis le monticule s'effondre sur place, et ce sont les molécules d'à côté qui s'assemblent pour former un nouveau monticule voisin.
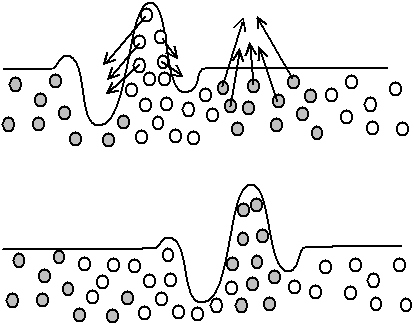
Fig. 2.7 - Les molécules d'eau bougent pour venir former un monticule (la vague),
mais reprennent leur place une fois la vague passée
On remarque souvent que l'on n'a pas une seule vague, mais une succession de plusieurs vagues. Par exemple, lors d'un plongeon dans une piscine, la montée ne se fait pas tout d'un coup mais par petits morceaux. Les vagues sont alors quasiment toutes identiques, elles ont notamment à peu près la même vitesse et à peu près la même largeur ; la largeur moyenne correspond de plus à la distance entre les crêtes voisines. On appelle donc cette distance moyenne la pseudo longueur d'onde, que l'on note en général avec la lettre grecque lambda indice m (lm) -- pseudo car cette valeur est légèrement différente pour chaque vague.
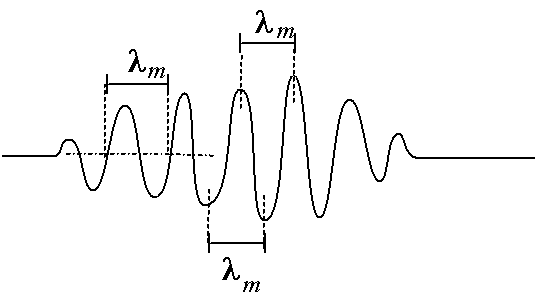
Fig. 2.8 - Succession de vagues
et pseudo longueur d'onde lm
Parfois, le phénomène qui produit la vague se répère régulièrement à l'indentique ; on dit que le phénomène est périodique. On appelle période, et on note T, le temps (en secondes) qui sépare deux répétitions successives du phénomène ; on dit par exemple que la période de rotation de la Terre est de 24 h, soit 86 400 s. On parle également parfois de cycle pour désigner une période.
On appelle fréquence du phénomène l'inverse de la période, que l'on exprime en Hertz (1 Hz = 1 s-1), que l'on note par la lettre grecque nu (n)
n = 1/TLa fréquence de rotation de la Terre est donc de 1,16.10-5 Hz ;
Comme le phénomène est rigoureusement identique à chaque fois, les vagues qui vont se succéder seront exactement pareilles. Notamment, la largeur, la distance entre les crêtes, sera à chaque fois exactement la même, on parlera donc de longueur d'onde notée lambda (l). La hauteur maximale par rapport à la moyenne est la même pour toutes les vagues, et est appelée amplitude A ; c'est également la profondeur au creux de chaque vague, et l'amplitude crête à crête est 2A.
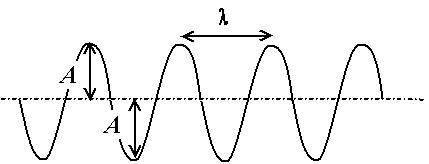
Fig. 2.9 - Vagues toutes identiques,
provenant d'un phénomène périodique
Cette régularité rigoureuse ne peut être qu'artificielle, par exemple, obtenue en faisant entrer/sortir un objet de l'eau, ou bien avec un dispositif d'air pulsÚ ; cependant, dans certains cas, on peut considérer pour simplifier qu'un phénomène naturel est périodique, notamment sur de courtes durées.
Si l'on prend une photo à un instant t donnÚ, on obtient la représentation de la hauteur h d'eau en fonction de la position x. On voit que si l'on se déplace d'une longueur d'onde selon la direction de progression des vagues, on retrouve la même hauteur d'eau. On parle donc de périodicité spatiale.
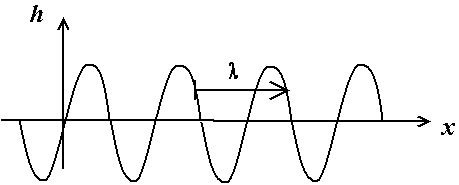
Fig. 2.10 - périodicité spatiale de la courbe h(x)
à t donné
Si l'on prend un point fixe (x donné) par rapport à la source périodique de vagues, alors les vagues arrivent à ce point à la même fréquence que la fréquence d'émission (si la source crée 1 vague par seconde, il arrive une vague par seconde au point fixe). Si par exemple on prend un bouchon de pêche et que l'on enregistre sa hauteur en fonction du temps, on obtient la même hauteur h toute les T secondes. On parle donc de périodicité temporelle.
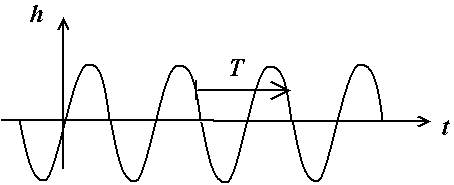
Fig. 2.11 - Périodicité temporelle de la courbe h(t)
à x donné
Du fait de cette double périodicité, on voit les vagues (avec une période spatiale) avancer de sorte qu'après une période, elle ont avancé d'une longueur d'onde (on retrouve exactement la même figure). La vitesse d'avancement V des vagues est donc
V = l/T = l.n
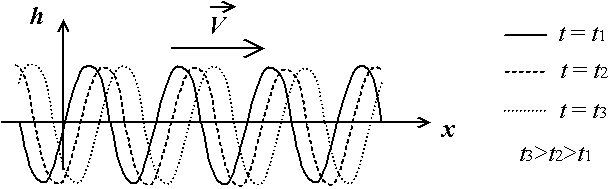
Fig. 2.12 - Double périodicité et vitesse de progression des vagues
On a donc un "ruban ondulé" qui s'avance, cette onde est donc appelée onde progressive
Les vagues, une forme d'ondes, sont donc une adaptation du milieu (l'eau) à une variation des conditions extérieures. Il y a un transport d'énergie associé à la vague, mais pas un transport de matière. Dans le cas de phénomènes périodiques, les vagues sont toutes identiques, et caractérisées par :