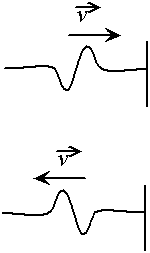
Fig. 3.1 - Réflexion de la vague sur le bord de la piscine vue en coupe
L'expérience nous montre que lorsque la vague frappe le bord de la piscine de face, elle repart en arrière ; c'est la réflexion.

Fig. 3.1 - Réflexion de la vague sur le bord de la piscine
vue en coupe
Si elle ne se présente pas face au bord, elle est réfléchie de sorte que le front fasse le même angle avec le bord après réflexion.
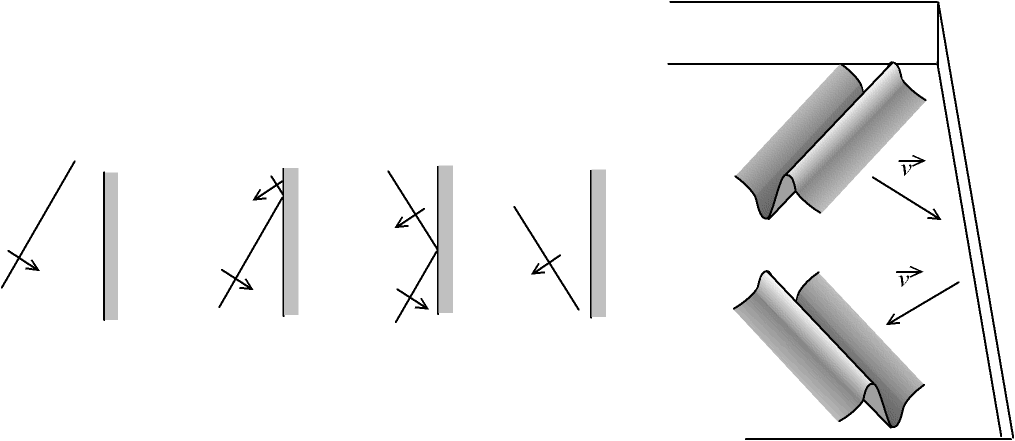
Fig. 3.2 - Réflexion de la vague sur le bord de la piscine
lorsque le front n'est pas parallèle au bord
Si l'on considère la droite qui figure la direction de progression, les droites avant et après réflexion sont symétriques par rapport au bord, comme si c'était la trajectoire d'une boule de billard rebondissant ; on appelle ceci la réflexion de Descartes1.
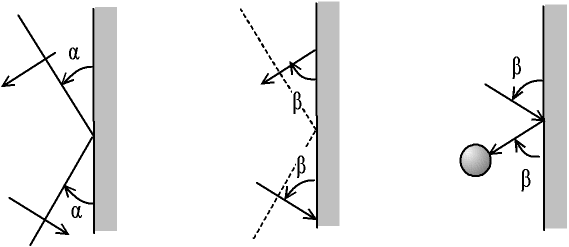
Fig. 3.3 - Réflexion de Descartes :
les fronts font le même angle a avec le bord,
les directions font le même angle b avec le bord,
analogie avec le rebond d'une boule de billard
La réflexion est en fait un cas particulier de la diffraction (cf. paragraphe suivant).
Note
1 - René Descartes, philosophe, mathématicien et physicien français (1596-1650)
retour
Lorsque que des vagues rencontrent un obstacle, elles sont perturbées, c'est ce que l'on appelle la diffraction ; deux cas se présentent :
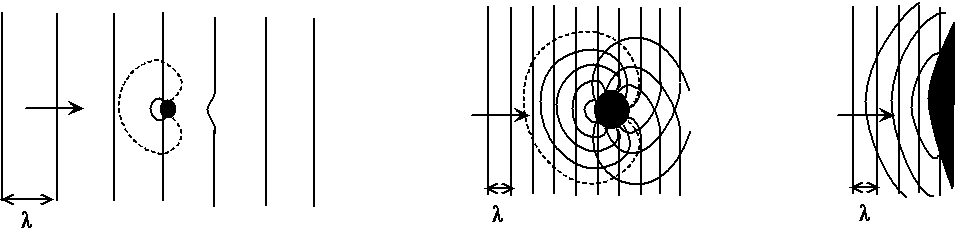
Fig. 3.4 - Diffraction :
perturbations faible si l'objet est très petit,
perturbations dans tous les sens
si la taille de l'objet est de l'ordre de grandeur de la longueur d'onde des vagues,
réflexion si la taille de l'objet est grande devant la longueur d'onde des vagues
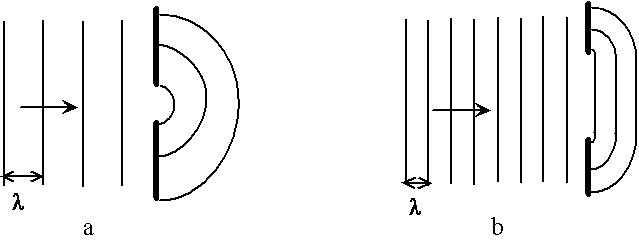
Fig. 3.5 - Diffraction par un trou :
a - front courbe si le trou est petit devant la longueur d'onde des vagues ;
b - présence d'un front droit si la trou est assez grand
par rapport à la longueur d'onde des vagues
Lorsque deux vagues se rencontrent, elles se superposent, les hauteurs s'ajoutent -- ajouter dans le sens algébrique du terme, c'est à dire que deux "bosses" s'ajoutent (interférence constructrice), deux "creux" s'ajoutent (interférence constructrice), mais un "creux" et une "bosse" se retranchent (interférence destructrice).
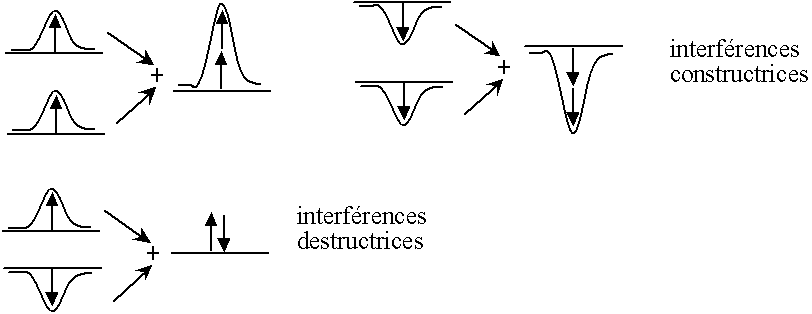
Fig. 3.6 - Lorsque les vagues se superposent
interférences constructrice et destructrice
Autrement dit, selon les cas, elle peuvent s'amplifier, on parle alors d'interférences constructrices ; dans d'autres cas, elle peuvent s'annuler, on parle alors d'interférences destructrices.
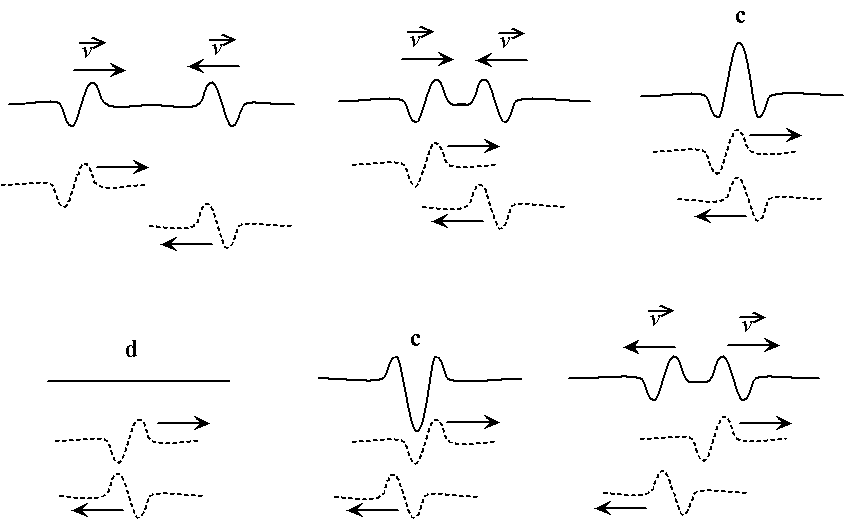
Fig. 3.7 - Interférence de deux vagues se croisant,
interférence constructrice (c) et destructrice (d)
Le cas le plus intéressant est celui de vagues périodiques. Pour illustrer ce phénomène, on considère souvent trois cas typiques, les vagues ayant les mêmes amplitudes :
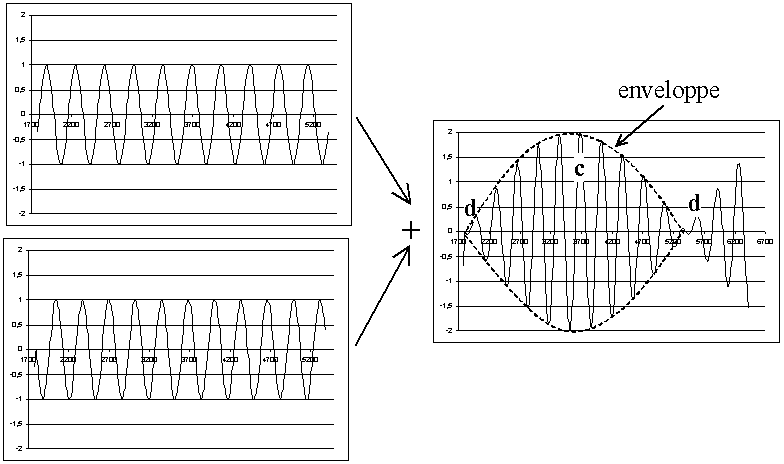
Fig. 3.8 - Interférence de vagues périodiques
de fréquences légèrement différentes :
interférences constructrices (c), destructrices (d) et
enveloppe globale
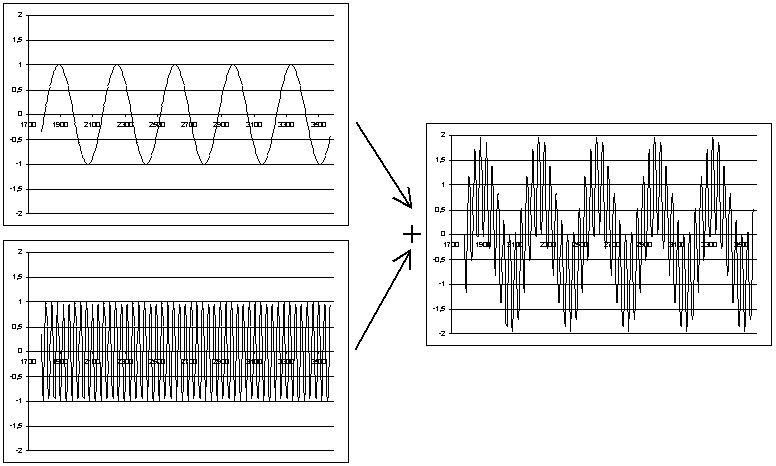
Fig. 3.9 - Interférence de vagues périodiques
de fréquences très différentes :
modulation de la basse fréquence par la haute fréquence
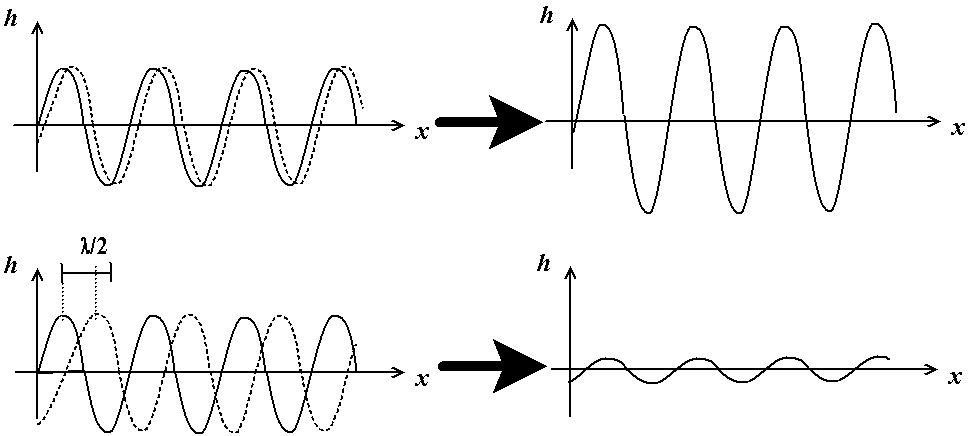
Fig. 3.10 - Interférence de vagues périodiques
de même fréquences mais décalées ;
interférences constructrices si le décalage est faible,
destructrices si il est proche de l/2
Dans le cas d'un "train de vagues" qui est réfléchi par le bord de la piscine, les vagues déjà réfléchies interfèrent avec les vagues qui arrivent. Les vagues réfléchies sont alors identiques au vagues qui arrivent (elles sont symétriques), mais elles sont déphasées, on a donc une succession dans le temps d'interférences constructrices et destructrices.
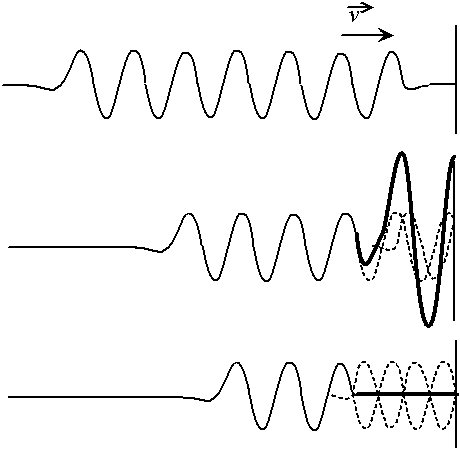
Fig. 3.11 - Interférence de vagues incidentes et de vagues réfléchies,
succession d'interférences constructrices et destructrices
Dans le cas où le bassin est petit et où l'onde s'étend sur toute la largeur, on a donc en permanence ce phénomène. On voit qu'en fait à certains endroits, les interférences sont toujours destructrices, on parle de noeuds de déplacement (la surface est "nouée" à cet endroit), et qu'à d'autres endroits, on atteint des hauteurs maximales, on parle alors de ventre de déplacement (en raison de la forme "ventrue"). La surface de l'eau est contenue dans une enveloppe, les vagues montent et descendent "sur place", sans se déplacer. Comme les vagues sont piégées par les bords du bassin, on parle d'ondes stationnaires par opposition aux ondes progressives (cf. 2.5).
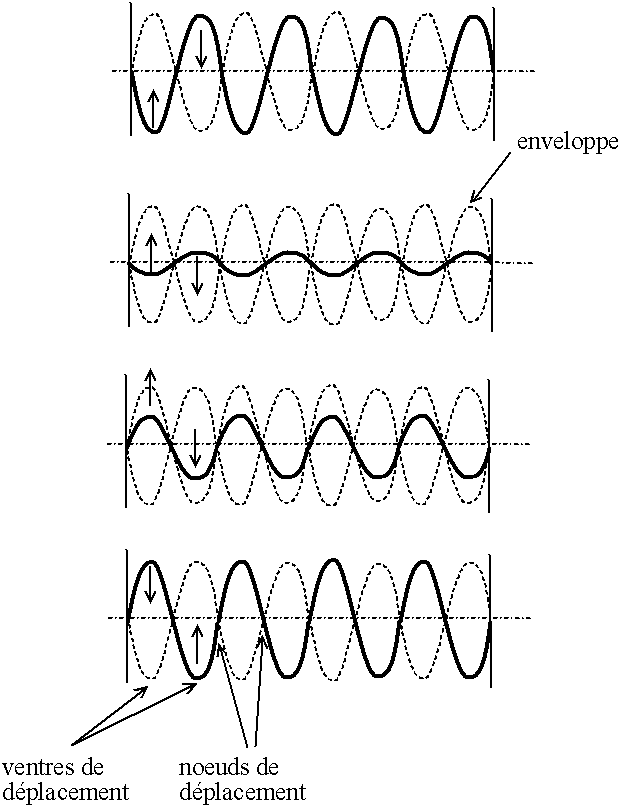
Fig. 3.12 - Onde stationnaire : enveloppe, ventres et noeuds de déplacement
Il ne s'agit pas de parler ici des sinus (ce n'est pas de l'anatomie) mais de la fonction mathématique. Si l'on considère, dans le plan géométrique, le cercle centré en O et de rayon 1 (appelé cercle trigonométrique), alors, le sinus d'un angle a est l'ordonnée du point du cercle correspondant à cet angle.
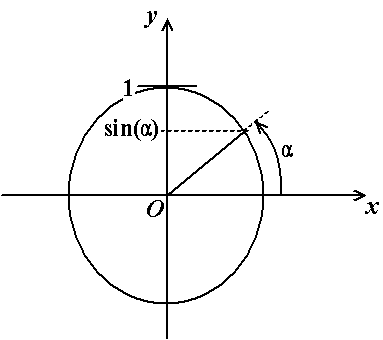
Fig. 3.13 - Définition de la fonction sinus
Par exemple, si l'on prend une roue de vélo de rayon r tournant à vitesse constante avec une fréquence n, et que l'on appelle h l'altitude de la valve de gonflage, on a :
h(t) = R + R.sin(2pn.t + a)NB : les angles sont exprimés en radians, 180o = p radians.
À l'instant initial t = 0, la valve est à l'altitude h(0) = R + R.sin(a), a est appelé phase à l'origine. On appelle pulsation la quantité notée w (oméga minuscule) :
w = 2pn = 2p/Tc'est la vitesse angulaire, exprimée en radians par seconde.
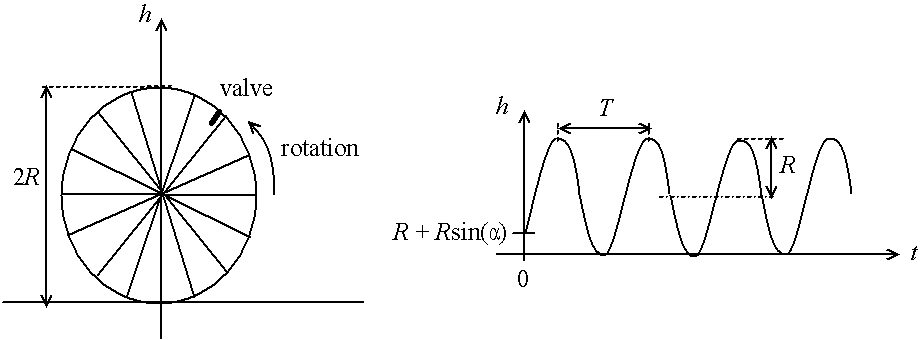
Fig. 3.14 - La hauteur de la valve : une fonction sinus
C'est une fonction périodique (elle prend la même valeur toutes les T secondes), d'amplitude R.
Dans les phénomènes périodiques où il y a une rotation, comme par exemple le mouvement des astres ou bien la production d'électricité par un alternateur (dynamo de vélo, centrale thermique classique ou nucléaire...), cette fonction sinus décrit parfaitement le phénomène. Cependant, du fait de sa simplicité et de ses propriétés intéressantes, cette fonction sert également de modèle à la plupart des phénomènes périodiques quels qu'ils soient. On peut en effet montrer qu'un phénoméne périodique quelconque peut se décomposer en une superposition de phénomènes sinusoiïdaux simples (développement en séries de Fourier2).
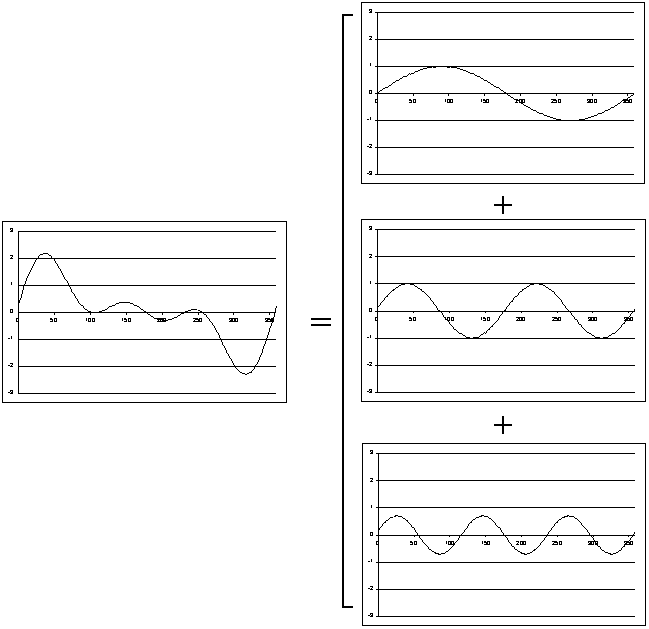
Fig. 3.15 - Décomposition d'une fonction périodique complexe
en fonctions sinusoïdales simples
Dans le cas d'une onde à front droit, si l'axe des x est perpendiculaire au front et orienté dans le sens de la progression (cf. 2.5), on peut écrire la hauteur H en fonction de l'emplacement x et du temps t :
où a (alpha) est une constante appelée phase à l'origine ; en choisissant bien l'origine des temps et des distances, on peut prendre alpha nul, mais cela n'est possible que si on ne considère qu'une seule onde.
H(x,t) = A. sin[2p(t/T - x/l) + a] = A. sin[2p(n.t - x/l) + a]
On peut définir la pulsation omega (en radians par seconde)
w = 2.p/T = 2.p.nainsi que le nombre d'onde k (en radians par mètre)
k = 2.p/ll'équation de l'ond s'écrit alors :
H(x,t) = H0. sin(w.t - k.x + a)Ainsi, l'interférence de deux ondes H1 et H2 s'écrit simplement de manière mathématique
[H1+H2](x,t) = A1. sin(w1.t - k1.x + a1) + A2. sin(w2.t - k2.x + a2)On retrouve ainsi très bien les phénomènes d'interférence, d'ondes stationnaires et de diffraction.
Note
2 - Joseph Fourier, mathématicien français (1768-1830)
retour
Lorsque deux ondes se rencontrent, les hauteurs s'ajoutent (et se retranchent), on parle d'interférences.
Lorsqu'une onde rencontre un obstacle, elle est réfléchie, on parle alors de diffraction :
Lorsqu'une onde est "piégée" dans un bassin, il se forme une onde stationnaire : les creux et les bosses se forment toujours aux mêmes endroits (appelés ventres de déplacement), la surface est épinglée entre deux ventres (ce sont les noeuds de déplacement).
Les ondes périodiques peuvent se modéliser avec la fonction sinus, ce qui permet de calculer facilement les effets d'interférence, de diffraction et d'ondes stationnaires.
Un autre site :
SCIO, site de vulgarisation de la physique