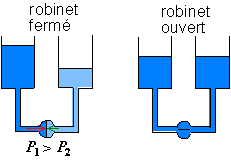
Fig. 4-1 Vases communicants : lorsque le robinet est fermé, la pression est différente de chaque côté du robinet, lorsqu'il est ouvert, le niveau est le même des deux côtés
| Forces et pression | Atmosphère | Lois physiques | * | Pompes, détendeurs | Mouvement | Vent et ondes | Physique |
Si l'on plonge dans l'eau, le poids de l'eau au-dessus de nous s'ajoute au poids de l'air, la pression que l'on subit augmente donc. D'après ce qui a été dit au paragraphe 2, on voit que la pression atmosphérique équivaut à la pression d'une colonne de 10 m d'eau, donc sous 10 m d'eau, on subira une pression double de la pression atmosphérique (1,01 bar dû à la pression de l'air, 1,01 bar dû à la pression de l'eau).
Comme pour l'air, la pression de l'eau s'exerce de la même manière dans toutes les directions.
La loi permettant de calculer la pression de l'eau est différente à celle utilisé pour l'air. En effet, contrairement à l'air, l'eau est incompressible (enfin, elle l'est mais très peu) : prenez une seringue sans aiguille, mettez de l'air de dans et bouchez-la avec votre doigt, vous verrez que l'on peut enfoncer le piston de plusieurs mm. Recommencez en ne mettant que de l'eau dans la seringue, le piston ne bougera pas (ou très peu, mais c'est la chair de votre doigt qui se comprime, pas l'eau).
La pression de l'eau (et des liquides en général) n'est donc quasiment pas reliée au volume et à la température. Au repos (si l'eau est immobile), elle est imposée par la hauteur d'eau, et par la pression de l'air au-dessus. Ainsi, la pression dans les tuyaux d'eau domestique est imposée par la hauteur du château d'eau.
En présence d'une pompe, c'est la pompe qui impose la pression. Si la pression d'un gaz détermine la quantité que l'on peut en mettre dans un volume fermé (pneu, bouteille de gaz...), ce n'est pas le cas d'un liquide. Par contre, la pression en sortie de pompe détermine la hauteur à laquelle on peut faire monter l'eau en refoulement (dénivellation des tuyaux) et la force de sortie de l'eau (vitesse, hauteur du jet...).
| début |
Si l'on prend deux bocaux remplis d'eau, avec un conduit d'eau entre les deux, alors la niveau dans les deux bocaux sera le même. Mais attention : le conduit doit être rempli d'eau, et en communication avec l'eau des deux bocaux. C'est ce principe qui permet le «siphonnage». Expliquons ceci d'un peu plus près.
Supposons deux bocaux, mis à la même hauteur, reliés par en-dessous par un conduit. On met un robinet au milieu du conduit, et on remplit les deux bocaux avec un niveau différent. Comme la colonne d'eau est plus élevée d'un côté que de l'autre, la pression au niveau du robinet est aussi plus élevée. Ainsi, lorsque l'on ouvre le robinet, l'eau qui a la plus forte pression pousse l'eau qui a une pression plus faible, et les niveaux s'équilibrent.

Fig. 4-1 Vases communicants :
lorsque le robinet est fermé,
la pression est différente
de chaque côté du robinet,
lorsqu'il est ouvert,
le niveau est le même des deux côtés
Notons que ceci ne dépend que de l'altitude de la surface de l'eau, et pas de la quantité d'eau totale. En effet, si un des bocaux est plus large, la paroi du bocal est aussi plus grande ; or, c'est cette paroi qui reçoit l'effort, seule l'eau du bocal au-dessus du conduit transmet l'effort à l'eau du conduit, le poids du reste de l'eau ne compte pas. Cela ne dépend pas non plus de l'orientation de l'ouverture du conduit, puisque la pression est la même dans toutes les directions.
Si le diamètre du conduit change, cela ne pose pas non plus de problème. En effet, il y a plus d'eau du côté du conduit qui a un gros diamètre donc plus de force, mais la force supplémentaire est supportée par la paroi du conduit à l'endroit du rétrécissement.
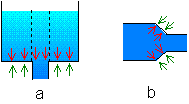
Fig. 4-2 La pression dans le conduit
ne dépend que de la hauteur d'eau :
a - le poids de l'eau (flèches rouges)
est soutenu par les parois du vase (flèches vertes),
seul le poids de l'eau au-dessus de l'ouverture
crée la pression dans le conduit
b - si le diamètre du conduit change,
l'excès de force (flèches rouges) est soutenu
par les parois du conduit (flèches vertes),
la pression est la même partout
Si maintenant le conduit passe au-dessus du niveau d'eau : cela ne change rien (tant qu'il n'y a pas d'air dans le conduit), la pression à l'entrée du conduit (bas du vase de gauche dans le dessin ci-dessous) est plus forte que la pression au sommet du conduit, et donc cela pousse l'eau dans le conduit, tant que les deux vases ne sont pas au même niveau. On notera que dans la partie du conduit située au-dessus du niveau de l'eau dans le bocal, la pression de l'eau est inférieure à la pression atmosphérique.
Au début, si le vase de droite est vide, le pression à la sortie est la pression de l'air, qui est plus faible que la pression de l'eau (puisque la pression de l'eau résulte de la pression de l'air et du poids de la colonne d'eau), donc l'eau sort. Plus l'eau monte dans le vase de droite, plus la pression augmente au niveau de la sortie du conduit, lorsque les pressions s'équilibrent, l'eau s'arrête de couler. C'est le principe du siphonage.
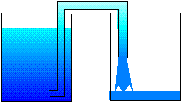
Fig. 4-3 Siphonnage :
l'eau coule tant que les deux vases ne sont pas au même niveau.
Toutefois, cela ne marchera plus si le conduit monte à plus de 10 m de hauteur : la pression de l'eau au bas du bocal ne sera plus suffisante pour faire monter l'eau jusqu'au sommet du conduit.
| début |
On a supposé jusqu'ici que les deux vases étaient à l'air libre, donc avaient une pression atmosphérique (1,01 bar) au-dessus d'eux. Supposons maintenant que l'on ferme un des vases de manière étanche.
La pression sous l'eau est la contribution du poids de l'eau et de la pression de l'air au-dessus de l'eau. Si l'on injecte ou que l'on retire de l'air dans le vase fermé, il se crée alors un déséquilibre, l'eau va bouger pour rétablir l'équilibre. Ce faisant, il y aura une différence de niveau entre les deux vases. Cette différence de niveau permet de mesurer la différence de pression : une différence de hauteur de 10 m correspond à une différence de pression de 0,981 bar (soit env. 1 bar), une différence de pression de 1 mm correspond à une différence de pression de 0,981 Pa (soit env. 1 Pa). Certains expriment parfois les faibles pression par la hauteur de colonne d'eau qui en résulte en mm (mmCE).
Prenons maintenant un liquide plus dense, comme le mercure. Un litre de mercure a une masse 13 fois plus élevée qu'un litre d'eau. Donc, pour une même différence de pression, on a une hauteur 13 fois plus petite. Ainsi, une différence de pression de 1 bar correspond à une hauteur d'environ 76 cm de mercure. C'est la raison pour laquelle on exprime parfois la pression atmosphérique par la hauteur de la colonne de mercure en cm ou en mm (cmHg ou mmHg).
Ce principe est utilisé pour les baromètres atmosphériques en U (le mercure est maintenant interdit pour des raisons de toxicité).
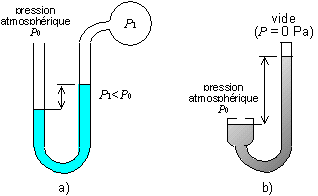
Fig. 4-4 Baromètres en U :
a) la différence de niveau permet de mesurer
la différence de pression
b) baromètre à mercure
pour mesurer la pression atmosph´rique
(par rapport au vide)