| précédent |
sommaire |
Éléments de cristallographie - 3
3 --- Pour aller plus loin...
3.2 - Groupes d'espace
Le groupe d'espace est désigné
soit par son numéro d'ordre, de 1 à 230 :
- structures tricliniques ; 1 à 2 ;
- " monocliniques ; 3 à 15 ;
- " orthorhombique ; 16 à 74 ;
- " tétragonal (quadratique) ; 75 à 142 ;
- " trigonales (rhomboédriques) ; 143 à 167 ;
- " hexagonales ; 168 à 194 ;
- " cubiques ; 195 à 230.
Mais les cristallographes utilisent la plupart du temps les symboles de
Hermann-Mauguin4 (1935),
qui décrivent les symétries de ce groupe ;
- d'abord la lettre désignant la présence ou non d'atomes au centre de la maille et des faces,
P, F, I,
A, B, C ou R ;
ceci indique les translations possibles ;
- des chiffres positifs (
1, 2, 3, 4 ou 6),
indiquant les rotations possibles en fraction de tour ;
le chiffre 2 indique une invariance par rotation d'1/2 tour autour d'un axe,
le chiffre 3 indique une invariance par rotation d'1/3 de tours...
le chiffre 1 indique que le cristal n'a aucune symétrie particulière
autre que l'identité (réseau triclinique P1) ;
- des nombres négatifs, le signe moins est symbolisé par une barre au-dessus du nombre
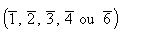 ;
ils indiquent que la structure est invariante par une inversion,
c'est à dire l'association d'une symétrie centrale
et d'une rotation d'une fraction de tour ;
-1 indique une invariance par symétrie centrale,
-6 une invariance par symétrie centrale suivie d'une rotation d'1/6 de tour ;
p.-ex. réseau triclinique
;
ils indiquent que la structure est invariante par une inversion,
c'est à dire l'association d'une symétrie centrale
et d'une rotation d'une fraction de tour ;
-1 indique une invariance par symétrie centrale,
-6 une invariance par symétrie centrale suivie d'une rotation d'1/6 de tour ;
p.-ex. réseau triclinique 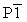 ;
dans le cas de la "triade" des réseaux cubiques
(inversion d'ordre 3 autour de la grande diagonale),
le signe moins peut être omis, on écrit indifféremment
;
dans le cas de la "triade" des réseaux cubiques
(inversion d'ordre 3 autour de la grande diagonale),
le signe moins peut être omis, on écrit indifféremment
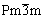 et
et Pm3m ;
- des lettres
m, chaque lettre symbolisant une invariance
par une symétrie selon un plan (miroir) ;
une barre de fraction entre un nombre et la lettre m indique
que le plan de symétrie est perpendiculaire à l'axe de rotation ;
notons qu'une réflexion est équivalents à une inversion d'ordre 2
(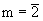 ) ;
) ;
- des couples de nombres dont le deuxième est en indice
nz,
indiquant une invariance par un mouvement de vis :
combinaison d'une rotation de 1/n tour selon un axe
et d'une translation de z/n fois le vecteur de cet axe ;
- un
a, un b, un c, n ou un d,
indiquant un glissement plan,
c'est à dire une symétrie plane associée à une translation
selon un vecteur du plan, soit d'une arrête (a, b ou c selon l'arrête),
soit de la demi-diagonale d'une face (n),
soit d'un quart de la grande diagonale de la maille (d pour diamant).
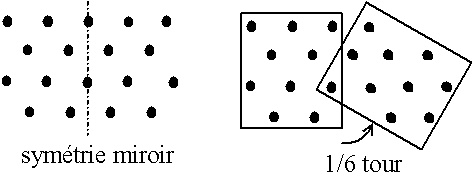
Fig. 3-3 Invariance du réseau
par une symétrie miroir (m) et une rotation d'1/6 tour (6)
L'ordre des symboles indique l'axe ou bien le plan de symétrie.
Pour caractériser un cristal,
on n'indiquera que le nombre minimum de symétries nécessaire
pour caractériser la structure
(si par exemple il y a une invariance par rotation d'1/4 de tour selon un axe,
on n'indiquera pas l'invariance par rotation d'1/2 tour qui en découle).
Si l'on ne considère que les symétries ponctuelles
(rotations, symétries planes, inversion et translation simple,
appelées ainsi car les axes de symétrie se coupent au centre de la maille),
on obtient 32 groupes de symétrie
(ceci ne prend pas en compte les translations, donc la première lettre n'est pas mentionnée) :
Tab. 3-2 Les 32 groupes de symétries ponctuelles
| Réseau cristallin |
Groupes de symétries ponctuelles |
Structures cristallographiques |
| Triclinique | 1, -1 | P-1 |
| Monoclinique | 2, m, 2/m | P 2/m, C 2/m |
| Orthorhombique | 2 2 2, m m 2, m m m |
P m m m, C m m m, F m m m, I m m m |
| Tétragonal (quadratique) | 4, -4, 4/m, 4 2 2, 4 m m, -4 2 m, 4/m m m |
P4/m, I4/m, P4/mmm, I4/mmm |
| Trigonal (rhomboédrique) | 3, -3, 3 2, 3 m, -3 m |
P -3, R -3, P -3 m 1, P -3 1 m, R -3 m |
| Hexagonal | 6, -6, 6/m, 6 2 2, 6 m m, -6 2 m, 6/m m m |
P 6/m, P 6/m m m |
| Cubique | 2 3, m -3, 4 3 2, -4 3 m, m 3 m |
P m -3, I m -3, F -3 m, P m -3 m, F m -3 m, I m -3 m |
Dans le cas de cristaux contenant plusieurs atomes,
les symboles ci-dessus sont modifiés ou complétés
afin de représenter les symétries supplémentaires.
Par exemple :
- corindon (Al2O3, trigonal)
R -3 c ;
- spinelle (MgAl2O4, cubique à faces centrées)
F d -3 m ;
- diamant (C, cubique)
F d 3 m.
Vous pouvez voir également la page sur les
symétries
cristallines de l'Université du Maine (Le Mans, France),
avec des animations interactives en Java.
La notation de Schönflies est largement utilisée dans le domaine de la description de molécules
(c'est à dire la description d'une molécule,
et non la description d'un assemblage de molécules),
ainsi que par les spectroscopistes ;
elle est donc mentionnée ici afin de faciliter la lecture de certains documents.
Elle est plus compacte, mais moins complète que la notation d'Hermann-Mauguin
(notamment, elle n'indique que les symétries ponctuelles et pas les translations).
Elle se compose habituellement d'une lettre, d'un nombre et d'une lettre en indice :
- symétries
Cn ; pour un axe (cyclique),
il s'agit d'un axe unique d'ordre n
(une rotation d'1/n tour laisse la structure invariante) ;
- symétries
Dn pour des axes perpendiculaires (dièdre),
il s'agit d'un axe d'ordre n perpendiculaire à n axes d'ordre 2 ;
- symétries cubiques :
T pour quatre axes (tétraèdre),
O pour huit axes (octaèdre) et
I pour vingt axes (icosaèdre, existe pour la description des molécules
mais n'existe pas pour la description des cristaux) ;
- symétries planes ; deux notations sont utilisées :
- une lettre en indice suit la symétrie de rotation (p.-ex.
C3h) ;
la lettre h en indice indique une symétrie plane (miroir)
selon un plan parallèle à l'axe de rotation (horizontal),
la lettre v selon un plan perpendiculaire à l'axe (vertical),
et la lettre d selon un plan diagonal ;
Sn, S indiquant la symétrie miroir
(Spiegel en allemand)
et n une invariance par une rotation d'ordre n autour de l'axe perpendiculaire au plan.
La présence d'un nombre m en exposant indique
que l'opération de symétrie est appliquée m fois.
Le tableau suivant donne la correspondance entre les symboles de Schönflies (à gauche)
et les symboles de Hermann-Mauguin (à droite).
Tab. 3-3 Correspondance entre la notation de Schönflies et celle d'Hermann-Mauguin
| Hexagonal |
Tetragonal |
Trigonal |
Orthorhombique |
Monoclinique |
Triclinique |
C6 | 6 | C4 | 4 | C3 | 3 |
| C2 | 2 | C1 | 1 |
C6v | 6 m m | C4v | 4 m m |
C3v | 3 m | C2v | 2 m m |
| |
C6h | 6/m | C4h - 4/m |
| | C2h | 2/m | |
C3h | -6 | | < | |
C1h | m (-2) | |
| S4 | -4 | S6 (C3i) | -3 |
| | S2 (Ci) | -1 |
D6 | 6 2 2 | D4 | 4 2 2 |
D3 | 3 2 | D2 | 2 2 2 |
| |
D6h | 6/m m m | D4h | 4/m m m |
| D2h | 2/m m m (m m m) |
| |
D3h | -6 2 m | | | |
| |
| D2d | -4 2 m | D3d | -3 m |
| | |
Pour les symétries cubiques,
T correspond à 2 3,
Th à m 3, O à 4 3 2,
Td à 4 -3 m, Oh à m 3 m
et I à 5 3 2
(donc impossible pour les cristaux, mais possible pour une molécule).
Notes
- 4 :
Carl Hermann, co-éditeur des premières table de structures cristallographiques en 1935 --
Charles Victor Mauguin, cristallographe français (1878-1958)
retour
- 5 :
Arthur Moritz Schönflies, mathématicien allemand (1853-1928)
retour
| début |
précédent |
suivant |
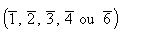 ;
ils indiquent que la structure est invariante par une inversion,
c'est à dire l'association d'une symétrie centrale
et d'une rotation d'une fraction de tour ;
-1 indique une invariance par symétrie centrale,
-6 une invariance par symétrie centrale suivie d'une rotation d'1/6 de tour ;
p.-ex. réseau triclinique
;
ils indiquent que la structure est invariante par une inversion,
c'est à dire l'association d'une symétrie centrale
et d'une rotation d'une fraction de tour ;
-1 indique une invariance par symétrie centrale,
-6 une invariance par symétrie centrale suivie d'une rotation d'1/6 de tour ;
p.-ex. réseau triclinique 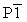 ;
dans le cas de la "triade" des réseaux cubiques
(inversion d'ordre 3 autour de la grande diagonale),
le signe moins peut être omis, on écrit indifféremment
;
dans le cas de la "triade" des réseaux cubiques
(inversion d'ordre 3 autour de la grande diagonale),
le signe moins peut être omis, on écrit indifféremment
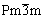 et
et 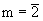 ) ;
) ;