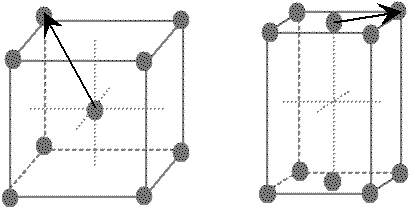
Fig. 3-1 Translations invariantes supplémentaires pour les structures autres que
P
Au paragraphe 2.1, nous avons décrit 7 formes de mailles, 7 réseaux élémentaires. Chaque réseau peut se décliner de quatre manières :
P (primitive) ;I (de l'allemand innenzentriert) ;F (face) ;C ;
C désigne les faces perpendiculaires à l'axe des z,
puisque le paramètre c est la dimension de la maille selon cet axe
-- on peut avoir de même A ou B ;R (rhomboèdre) ;
seules les mailles trigonales peuvent être R.
On obtient donc ainsi 14 réseaux de Bravais (cf. tableau 3-1).
Si l'on effectue une translation selon un vecteur de la base
ou une combinaison linéaire des vecteurs de la base,
on obtient le même réseau ;
cependant, la présence d'atomes en dehors des sommets
permet d'avoir d'autres translations laissant le réseau invariant :
des translations selon une demi-grande diagonale (structures centrées I)
ou bien la demi-diagonale d'une face (structure à faces centrées
F, A, B ou C).

Fig. 3-1 Translations invariantes supplémentaires
pour les structures autres que P
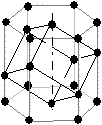
NB : la structure trigonale (rhomboédrique) est obtenue en étirant un cube selon une de sa grande diagonale ; de fait, si l'on regarde la maille dans cette direction, on voit un hexagone. Cependant, le système hexagonal est invariant par une rotation d'1/6 de tour, alors que le système trigonal est invariant par une rotation d'1/3 de tour.
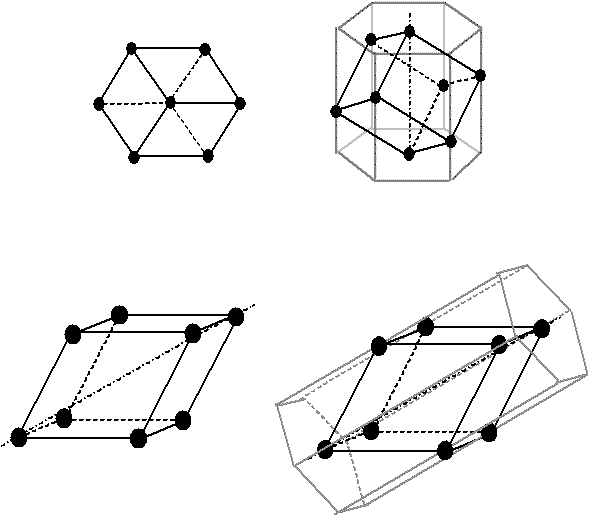
Fig. 3-2 Symétrie trigonale et sur-maille hexagonale,
vue selon la grande diagonale et vues en perspective
Ainsi, la structure trigonale a une maille qui semble dériver de la maille hexagonale, mais ayant une invariance de rotation d'1/3 de tour et non de 1/6, elle est bien différente.
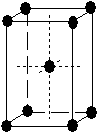
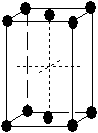
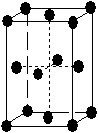
Tab. 3-1 Les 14 réseaux de Bravais
| Système | simple (P) |
centré (I) |
à 2 faces centrées (C) |
à faces centrées (F) |
structure rhomboédique ( R) |
| cubique | 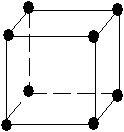 |
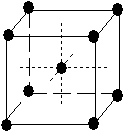 |
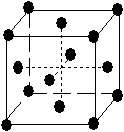 |
||
| hexagonal | 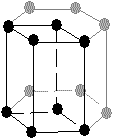 |
||||
| tétragonal (quadratique) |
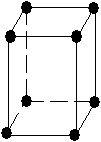 |
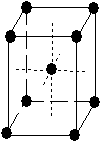 |
|||
| trigonal (rhomboédrique) |
 |
||||
| orthorhombique | 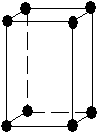 |
 |
 |
 |
|
| monoclinique | 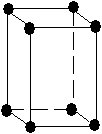 |
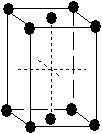 |
|||
| triclinique | 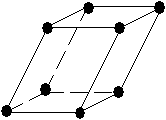 |
Vous pouvez voir également la page sur les réseaux de Bravais de l'Université du Maine (Le Mans, France), avec des animations interactives en Java.