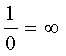.
Du fait de l'invariance par translation,
il y a une infinité de plans atomiques parallèles à un plan atomique donné.
Considérons une maille élémentaire munie de son repère
défini au paragraphe 2.3.
Alors, le plan d'orientation (hkl) le plus proche de l'origine mais ne passant pas par l'origine,
coupe l'axe des x en 1/h, l'axe des y en 1/k et l'axe des z en 1/l ;
si l'un des indices est nul, alors le plan est parallèle à l'axe,
avec la convention .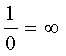
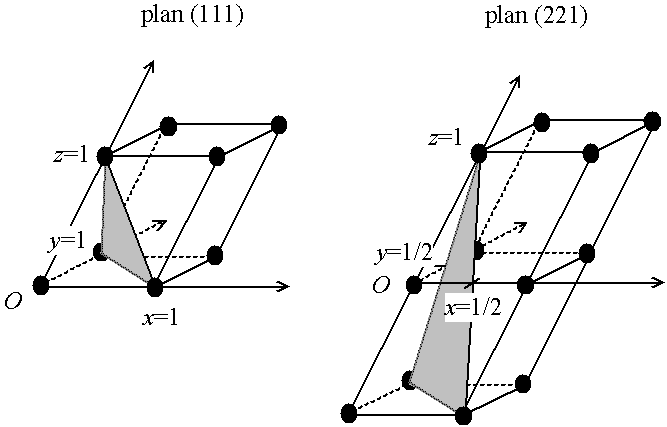
Fig. 3-8 Indice de Miller et interception des axes
Dans le repère de la maille, le plan a pour équation
h.x + k.y + l.z = Coù C est une constante.
Il peut être intéressant de repérer les directions, les droites, dans un cristal. C'est par exemple très utilisé dans le domaine de la déformation plastique (vecteurs de Burger).
DéfinitionDe même que pour les plans nodaux, on parle souvent de "rangées atomiques". Les indices de Miller d'une rangée sont notés entre crochets [uvw]. u, v et w sont des entiers qui sont les composantes d'un vecteur de la droite, les nombres négatifs étant notés avec une barre au-dessus. On parle aussi de direction cristallographique pour désigner les indices [uvw].
On appelle rangée nodale une droite de l'espace passant par des noeuds du cristal.
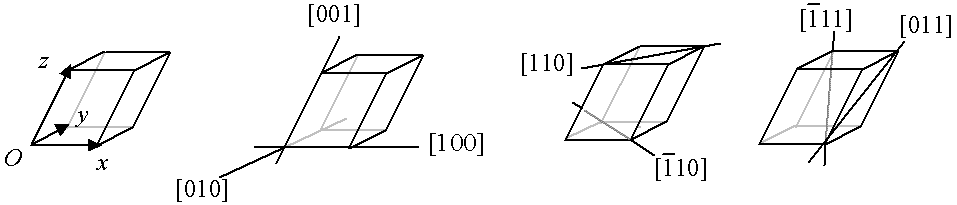
Fig. 3-9 Indice de Miller de quelques directions cristallographiques
dans une maille triclinique
Dans le cas des structures cubiques, on peut appliquer toutes les relations classiques de la géométrie et de la trigonométrie. On peut par exemple calculer aisément la distance inter-réticulaire :
où a est le paramètre de la maille.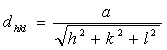
De plus, d'après les symétries des structures cubiques,
on voit que les plans (100), (010) et (001) sont équivalents.
De manière plus générale, si l'on considère les plan (hkl),
alors tous les plans obtenus par permutation des indices et par leur changement de signe sont équivalents
;
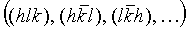on parle alors de famille de plans {hkl} (notation entre accolades).
Ainsi, la famille {110} comprend les plans
.
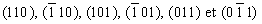De même, les directions cristallographiques obtenues
par permutation et changement de signe des indices de Miller
sont équivalentes,
on parle donc de famille de rangées <uvw> (notation entre brackets).
Ainsi, la famille <110> comprend les droites
![[110], [-110], [101], [-101], [011] et [0-11]](eq11.gif)
Mais ceci n'est malheureusement valable que pour les réseaux cubiques...