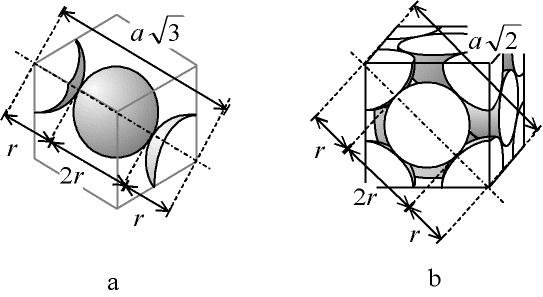Il s'agit là bêtement de géométrie dans l'espace. Connaissant les paramètres de maille, dans le cas de cristaux monoatomiques, on peut par exemple calculer la distance entre noyaux des atomes ; cette distance est de l'ordre de l'angström (soit 10-10 m) alors que le rayon d'un noyau est de 2 à 8 femtomètres (1 fm = 10-15 m), on peut donc considérer ceux-ci comme ponctuels.
Dans le cas le plus simple, les réseaux cubiques, il suffit de savoir que la diagonale d'une face est racine de 2 fois plus grande que l'arrête (théorème de Pythagore), et que la grande diagonale vaut racine de 3 fois l'arrête.
On peut aussi comparer le volume occupé par les atomes (en supposant que ce sont des sphères dures) et le volume de la maille, le rapport des deux étant la compacité ; elle est toujours inférieure à 1, une compacité de 1 signifierait qu'il n'y a aucun vide entre les motifs (les atomes).
NB : "racine(x)" désigne par la suite la racine carrée de x.
Fig. 4-6 Atomes a - sur la grande diagonale d'un cristal cubique centré
et b - sur la diagonale d'une face d'un cubique à faces centrées
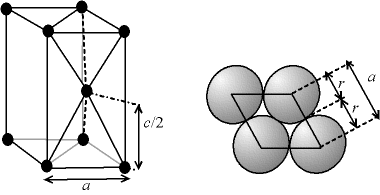
Fig. 4-7 Relation entre les paramètres a, c et r
dans une structure hexagonale compacte