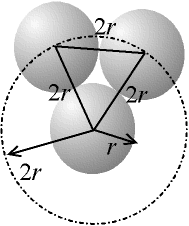
Fig. 4-8 Empilement compact sur un plan : la symétrie est nécessairement hexagonale
On remarque que la structure cubique à faces centrées et la structure hexagonale compacte on la même compacité (74 %). On a vu que les plans étaient de même nature, à symétrie hexagonal, or, c'est c'est le plus compact possible : si l'on cherche à mettre le maximum de sphères de rayon r autour d'une autre sphère dans un plan, les centres sont tous séparés d'une distance 2r, on forme donc un triangle équilatéral dont l'angle au sommet est 60o (1/6 tour). On a donc nécessairement une symétrie hexagonale.

Fig. 4-8 Empilement compact sur un plan :
la symétrie est nécessairement hexagonale
Nous invitons le lecteur à vérifier que c'est bien l'empilement le plus compact, par exemple en disposant des verres dans un carton (on peut en mettre plus de cette manière) ; cette disposition est dite "en quinconce" -- par cinq, elle rappelle en effet la disposition des points représentant la face "5" sur dé à six faces.
Les plans sont ensuite eux-même empilés de manière compacte, c'est en fait la compacité maximale que l'on puisse atteindre en empilant des boules.
En fait, il y a une infinité de manières d'agencer les plans, par exemple A/B/A/C... (lanthane), ou bien A/B/C/B/A..., ou encore A/B/C/B/C/A/C/A/B... (samarium), tous ces empilements auront la même compacité.
N'oublions cependant pas que les cristaux compacts ne sont qu'une imfime partie des cristaux pouvant exister, et que de plus les cristaux réels, loin d'être des empilements parfaits, sont pleins de défauts, mais c'est un autre sujet...
| début | précédent | suivant |
********** Fin **********