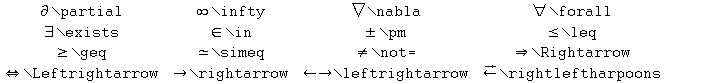
| Base | Caractères | Mise en forme 1 | Mise en forme 2 | Commandes | Environnements | * | Références | Biblio |
Les formules mathématiques sont la raison d'être de TeX. La syntaxe est proche de celle générée par l'éditeur d'équation de Sun StarWriter (StarOffice).
Nous allons construire des équations afin de voir la logique du système. Devant l'étendue du sujet, nous nous contenterons de donner quelques éléments.
Une équation se place entre deux signes dollar
« $ ».
Pour écrire une fraction,
nous utilisons la fonction \frac{dividende}{diviseur} :
$ \frac{a+b}{c-d} $
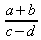
( »
et « ) »,
mais cela mettrait des petites parenthèses,
donc utilisables seulement sur une ligne simple.
Pour mettre des grandes parenthèses,
il faut mettre \left devant celle de gauche
et \right devant celle de droite :
$ \left( \frac{a+b}{c-d} \right)$
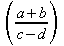
\{ et \},
et pour de grandes accolades : \left\{ et \right\}.
Les éléments en indice sont précédés
d'un trait en bas « _ »,
et les éléments en exposant
du chapeau « ^ » :
$a_{n}^{m}$
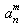
\cdot.
Les lettres grecques s'obtiennent en les écrivant en phonétique
avec une barre de fraction inversée devant :
$\Delta y = f'(x) \cdot \delta x$
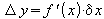
Les fonctions mathématiques classiques
sont précédées d'un « \ »
pour qu'elles figurent en lettres droites,
et non en italiques comme les variables :
\sin par exemple.
L'opérateur somme (sigma majuscule S)
s'écrit \sum ;
pour écrire les limites de la somme, il suffit de les metre en indice et exposant :
$\sum u_{n}$ ; $\sum_{i=1}^{n} (v_{i-1}+u_{i})$
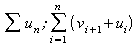
Il y a trois principaux types de formules mathématiques :
$ formule $
\[ formule \]
\begin{equation} et \end{equation}
Les nombres et les variables sont tapées tels quels,
ainsi que les symboles suivants :
+ - / =
pour la multiplication, la croix « × » est affiché par la fonction \times
et le point « · » par la fonction \cdot.
Pour les fractions, on utilise la syntaxe :
\frac{dividende}{diviseur}.
Les lettres grecques s'obtiennent en écrivant la lettre en phonétique avec une barre de fraction inversée devant :
\alpha \beta \gamma… \chi \psi \omega
notons que certaines lettres existent en deux écritures différentes :
\epsilon et \varepsilon,
\theta et \vartheta,
\pi et \varpi,
\rho et \varrho,
\sigma et \varsigma,
\phi et \varphi.
Lorsque les capitales sont différentes des majuscules romaines,
la lettre s'obtient de la même manière
mais en mettant une majuscule :
\Gamma \Lambda \Sigma \Psi \Delta \Xi \Upsilon \Omega \Theta \Pi \Phi
On dispose également de symboles mathématiques :
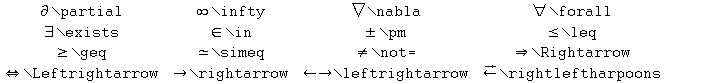
| Caractère | instruction LaTeX | Caractère | instruction LaTeX |
|---|---|---|---|
| ( | ( |
) | ) |
| { | \lbrace ou \{ |
} | \rbrace ou \} |
| [ | \lbrack |
] | \rbrack |
| < | \langle |
> | \rangle |
| | (valeur absolue) | | (tube, pipe) |
Les délimiteurs de grande taille (qui contiennent une fraction par exemple)
sont précédés de \left pour le délimiteur de gauche,
et de \right pour celui de droite.
Exemple :
\left \brack et \right \rbrack,
\left ( et \right )
Les fonctions qui sont « en clair » s'écrivent précédées d'un \
afin qu'elles s'affichent en lettres droites :
\sin \arcsin \cos \arcsos \tan \arctan \ln \log \lim \min \max \inf \sup …
La fonction racine carré s'écrit \sqrt{radicande},
la racine n e \sqrt[n]{radicande}.
Petits vecteurs : \vec{u} ;
grands vecteurs : \overrightarrow{AB}
barre (moyenne, valeur algébrique) : \bar{x}
chapeau : \hat{a} ;
grand chapeau (angles) : \widehat{AOB}
point au-dessus (dérivée selon le temps) : \dot{x} ;
double point : \ddot{x}
Le principe pour la somme s'applique également pour le produit,
le pi majuscule étant obtenu par la fonction \prod,
et l'intégrale avec \int.
On place les limites de la même manière
en les considérant en indice et en exposant.
Exemple :
$
\hat\sigma =
\sqrt{
\frac{1}{n-1} \cdot
\sum_{i=1}^{n} \left ( x - \bar{x} \right ) ^2
}
$
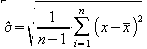
$
F(u,v,w)=
\int\int\int_{-\infty}^{+\infty}
f(x,y,z) \cdot
\exp \left (
2 \pi i(ux+vy+wz) \right )
\cdot dx \cdot dy \cdot dz
$
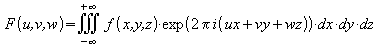
Le principe est le même que pour les tableaux
(environnement tabular).
On définit l'environnement par
\begin{array}{colonnes} et \end{array}.
Les colonnes sont délimitées par une perluettte « & »
et les lignes par une double barre de fraction inversée « \\ ».
On peut insérer des points horizontaux avec \cdots,
verticaux avec \vdots et diagonaux avec \ddots.
Exemple :
\[
\left (
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right )
\]

\[
\left (
\begin{array}{cccc}
1 & 0 & \cdots & 0 \\
0 & \ddots & & \vdots \\
\vdots & & \ddots & 0\\
0 & \cdots & 0 & 1 \\
\end{array}
\right )
\]

En ce qui concerne les réactions chimiques,
une réaction irréversible (flèche vers la droite)
s'écrit \longrightarrow,
et une réaction réversible (double-flèche)
s'écrit \rightleftharpoons.
Les éléments étant en lettres droites,
il faut utiliser la fonction \mathrm{}
(« romaines »)
en début de formule.
Exemple :
\[\mathrm{ H_{3}O^{+} + OH^{-} \rightleftharpoons 2H_{2}O }\] \[\mathrm{ \mathit{n} M + O_{2} \longrightarrow M_{\mathit{n}} O_{2} }\]
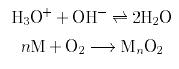
L'extension (package) amsmath
de l'association étatsuniennes de mathématiques
fournit des possibilités complémentaires.
Par exemple, pour les matrices,
plutôt que d'utiliser un grand délimiteur
puis l'environnement array,
on peut utiliser les environnements
pmatrix (matrice entre parenthèses),
bmatrix (matrice entre crochets) ou
vmatrix (matrice entre barres verticales).
Avec l'extension amsfont,
on dispose de polices de caractères supplémentaires.
On peut par exemple afficher les lettres à double barre
représentant les ensembles de nombres avec l'instruction
\mathbb, par exemple
\mathbb{N} pour les entiers naturels,
\mathbb{R} pour les réels,
\mathbb{C} pour les complexes.
suivant : Références
 |
 |
 |