| précédent |
sommaire |
Éléments de cristallographie - 2
2 -- Notions de cristallographie
2.4 - Symétries et groupes d'espace
Les cristaux ont été d'abord caractérisés par leurs symétries ;
on peut donc également classer les structures par les symétries qu'elles possèdent,
c'est à dire donner le groupe d'espace auquel elles appartiennent.
En raison des propriétés de l'espace géométrique,
il n'existent que 230 groupes d'espace en cristallographie.
Le groupe d'espace est désigné
soit par son numéro d'ordre (de 1 à 230),
soit par les symboles
d'Hermann-Mauguin1,
qui décrivent les symétries de ce groupe :
il s'agit d'une lettre majuscule suivie d'une succession de nombres et de lettres
(avec éventuellement des barres de fraction).
Sur des publications papier, les nombres négatifs sont indiqués avec une barre au-dessus
(p.-ex. 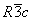 ),
et certains chiffres sont en index (p.-ex. 42).
Sous forme informatique, les symboles sont séparésd'un espace,
les nombres négatifs sont indiqués avec le signe moins devant,
et les nombres en indice sont accolés au nombre précédent
(tous les nombres sont inférieurs à 6, il n'y a donc pas de confusion possible).
Par exemple :
),
et certains chiffres sont en index (p.-ex. 42).
Sous forme informatique, les symboles sont séparésd'un espace,
les nombres négatifs sont indiqués avec le signe moins devant,
et les nombres en indice sont accolés au nombre précédent
(tous les nombres sont inférieurs à 6, il n'y a donc pas de confusion possible).
Par exemple :
Tab. 2-2 Notation d'Hermann-Mauguin sur papier et sur écran informatique
| composé | groupe d'espace |
| format papier | format informatique |
| Corindon Al2O3 | 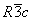 | R - 3 c |
| Troilite FeS | P 63/mmc | P 63/m m c |
Les groupes de symétrie sont décrits plus précisément
dans la partie 3.2.
Note
- 1 -
Carl Hermann, coéditeur des premières tables
de radio-cristallographie en 1935 -
Charles Victor Mauguin, cristallographe français (1878-1958)
retour
| début |
précédent |
suivant |
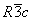 ),
et certains chiffres sont en index (p.-ex. 42).
Sous forme informatique, les symboles sont séparésd'un espace,
les nombres négatifs sont indiqués avec le signe moins devant,
et les nombres en indice sont accolés au nombre précédent
(tous les nombres sont inférieurs à 6, il n'y a donc pas de confusion possible).
Par exemple :
),
et certains chiffres sont en index (p.-ex. 42).
Sous forme informatique, les symboles sont séparésd'un espace,
les nombres négatifs sont indiqués avec le signe moins devant,
et les nombres en indice sont accolés au nombre précédent
(tous les nombres sont inférieurs à 6, il n'y a donc pas de confusion possible).
Par exemple :