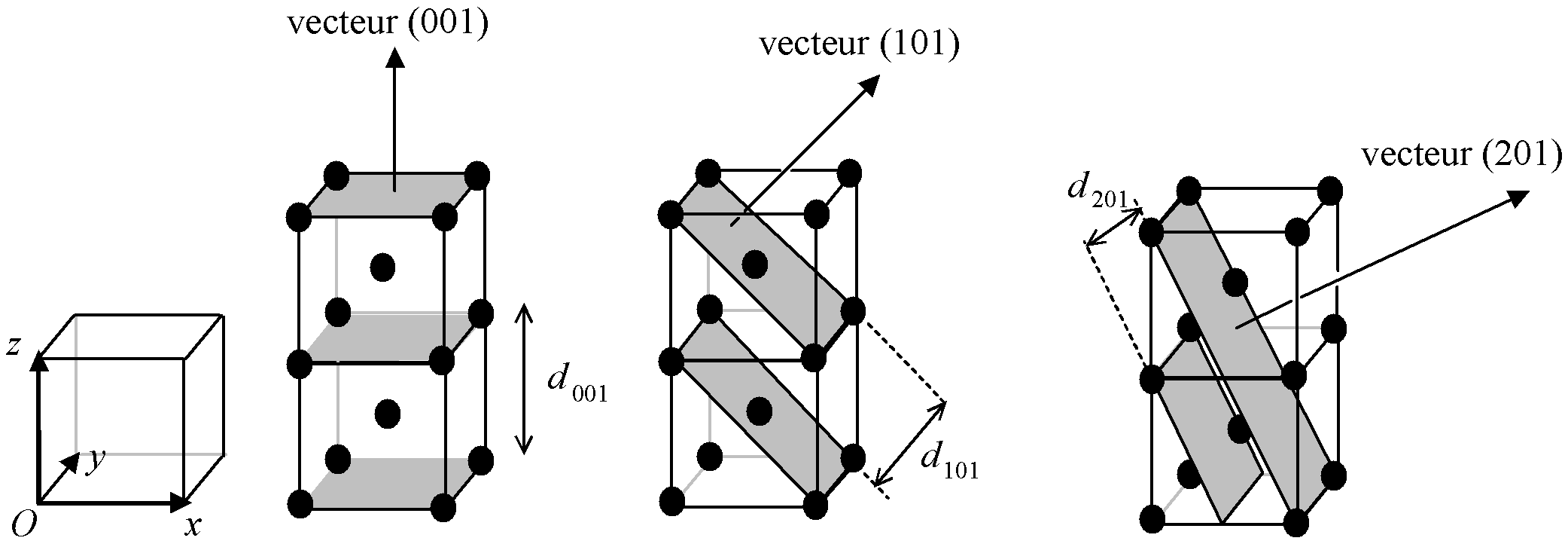
Fig. 2-8 Plans nodaux, vecteurs normaux et distance inter-réticulaire
Définition :Cette notion joue un rôle très important dans les phénomènes de diffraction ainsi que pour la déformation plastique. Étant donné que la plupart des motifs étudiés sont des atomes uniques, on parle souvent de "plan atomique". Un des problème de la cristallographie consiste donc à décrire ces plan, c'est à dire notamment à donner leur orientation dans l'espace. Cette orientation est donnée par trois nombres entiers mis entre parenthèse, dits "indices de Miller"1, et traditionnellement appelés h, k et l ; on parle ainsi de plans (100) (prononcer "un-zéro-zéro"), (110)... La première idée consiste donc à définir une base vectorielle liée au réseau. On prend pour vecteurs de la base les arrêtes de la maille élémentaire ; donc, en dehors des structures cubiques, la base est quelconque, c'est à dire ni orthogonale, ni normée. L'orientation d'un plan est décrite, comme en mathématiques, par la donnée de son vecteur normal. Dans le cas d'un réseau cubique, ce vecteur est perpendiculaire au plan. Dans le cas d'un réseau quelconque, il n'est plus perpendiculaire au sens "angle droit", mais si on déformait la maille pour la rendre cubique, alors il le deviendrait. Ce sont les coordonnées de ce vecteur qui forment les indices de Miller. Lorsque des coordonnées de vecteur sont négatives, on place une barre au dessus de l'indice de Miller correspondant : par exemple, le plan représenté par le vecteur de composantes (-1,1,2) sera noté
on appelle un plan nodal l'ensemble des noeuds situés sur un plan de l'espace.
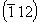(mais appelé "moins un-un-deux") ;
cependant, la barre au-dessus ne faisant pas partie des polices informatiques standard,
on le verra aussi souvent écrit (-112).
Pour des raisons géométriques évidentes,
si l'on change le signe des trois indices, on obtient le même plan,
(hkl) = (-h-k-l).
Du fait de l'invariance par translation du cristal, il y a une infinité de plans parallèles entre eux. La distance qui sépare deux plans parallèles voisins est appellée "distance inter-réticulaire", et est notée dhkl. On remarque que plus les indices de Miller sont élevés, plus les plans sont proches (plus dhkl est petit).
Fig. 2-8 Plans nodaux, vecteurs normaux et distance inter-réticulaire
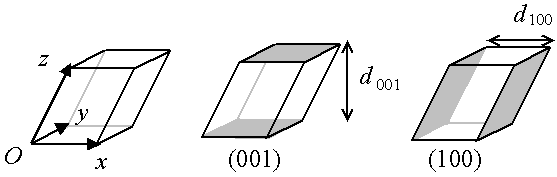
Fig. 2-9 Exemples de plans nodaux dans un réseau triclinique (quelconque)
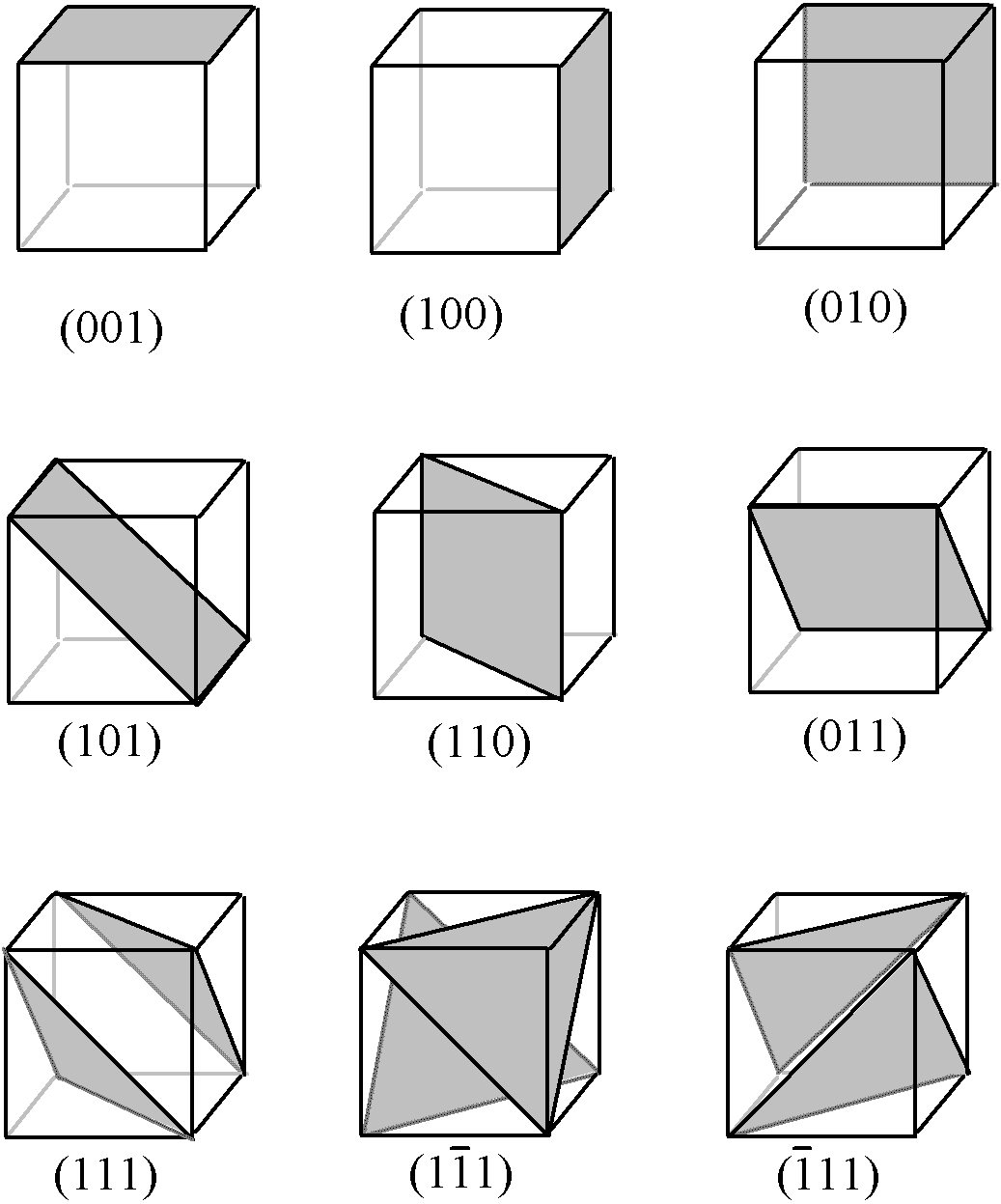
Fig. 2-10 Exemples de plans nodaux dans un réseau cubique
Dans le cas ou il y a des noeuds au centre des mailles ou des faces, il peut y avoir des "sous-plans" d'indices supérieurs :
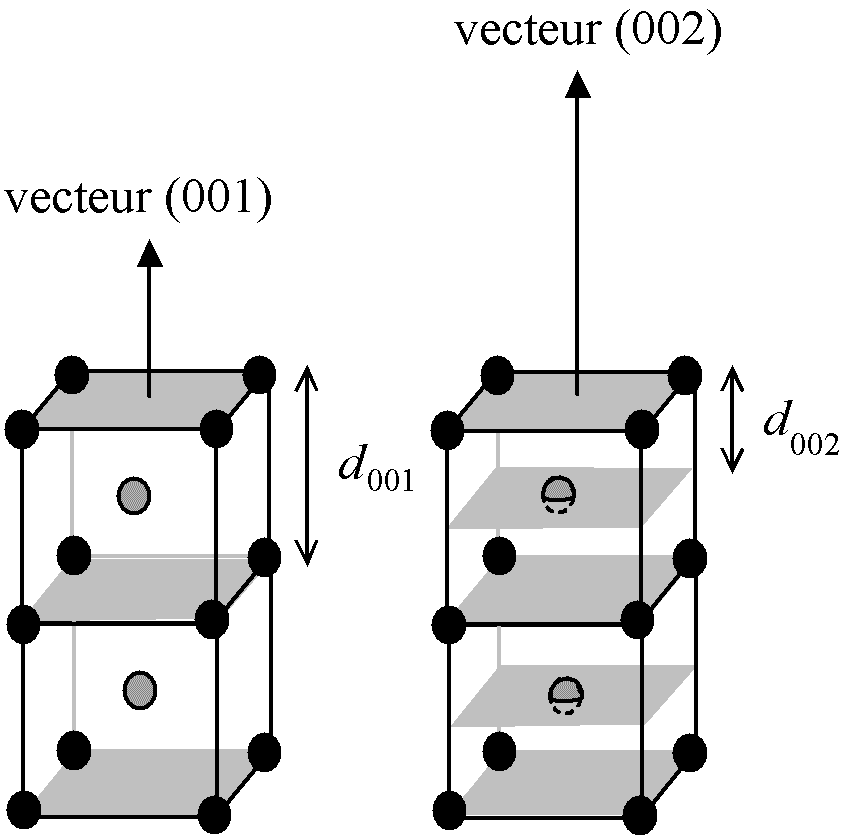
Fig. 2-11 "Sous-plans" de type (002) dans une structure cubique centrée
Vous aurez plus de détails dans la partie 3.4.
Note