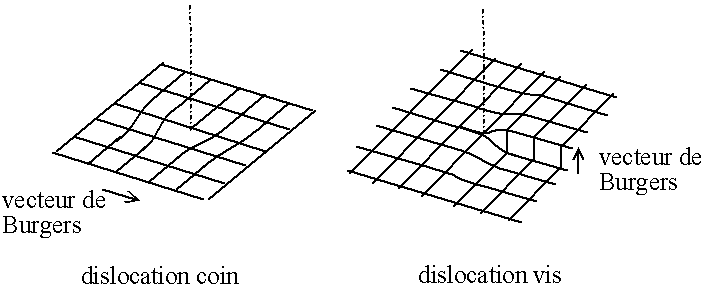
Fig. 3.1 - Vecteur de Burgers (de déformation) dans le cas d'une dislocation coin et d'une dislocation vis
| précédent |
La déformation propagée peut être représentée par un vecteur, appellé vecteur de Burgers. Ainsi, on dit que la dislocation est coin si le vecteur de Burgers est perpendiculaire à la ligne de dislocation, et qu'elle est vis si il est parallèle.

Fig. 3.1 - Vecteur de Burgers (de déformation)
dans le cas d'une dislocation coin et d'une dislocation vis
Le glissement consiste en une translation des atomes, la structure globale du cristal restant inchangée, donc un atome prend la place d'un autre atome. Comme la déformation est forcément un vecteur reliant deux atomes, c'est à dire un vecteur du réseau cristallographique, on peut utiliser les indices de Miller pour donner le vecteur de Burgers (cf. les notions de Plans nodaux et de Rangées nodales). Ainsi, on parle de dislocation [100] ou bien 1/2[111].
La contrainte extérieure exercée sur le cristal entraîne le déplacement d'atomes qui provoque le déplacement de la dislocation. On peut donc considérer que la contrainte fait elle-même bouger la dislocation. Intuitivement, on voit que :