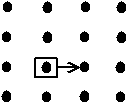
Fig. 2-1 Invariance par translation dans un réseau
Une grande partie de la matière solide (métaux, oxydes, minéraux, sels...) est sous forme cristalline.
Définition :
Cristal monoatomique : empilement infini et régulier d'atomes identiques.

Fig. 2-1 Invariance par translation dans un réseau
Le réseau est donc un objet mathématique descriptif. A chaque noeud de ce réseau se trouve un "motif", c'est à dire un objet physique, souvent un atome. Dans certains cas, le motif peut être une molécule (par exemple, I2 dans un cristal d'iode, H2O dans un cristal de glace, produit organique cristallisé comme le sucre...), voir une molécule très complexe. Il faut donc maintenant étendre la définition précédente :
Définition :On peut illustrer ces notions de motif et de réseau dans le cas d'un carrelage : les carreaux sont les motifs, et leurs emplacements sont les noeuds d'un réseau.
Cristal : un empilement infini et régulier de motifs identiques, un motif pouvant être un atome, plusieurs ou bien une molécule.
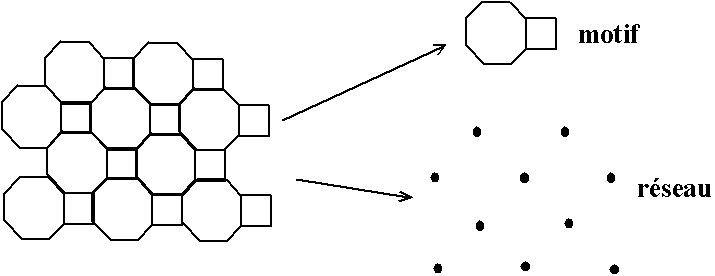
Fig. 2-2 Illustration de la notion de motif et de réseau dans un carrelage
NB : pour des raisons pratiques, nous représenterons en général le cas ou un motif est un atome unique.
La notion de réseau est née en géologie, avant que l'on ne connaisse les atomes ; Haüy1 et Bravais2, en étudiant la symétrie extérieure de certains cristaux et notamment le fait que le clivage se fasse selon certains plans, en déduisirent que "l'organisation interne" de la matière devait avoir les mêmes symétries.

Fig. 2-3 Symétries extérieures de cristaux de pyrite
(FeS2)
reflétant l'organisation interne de la matière
source :
minerals.net
Ceci fut confirmé en 1912 par les expériences de diffraction de rayons X sur la matière par Laue3 : la figure de diffraction étant elle-même un réseau ordonné, cela ne peut s'expliquer que s'il y a une périodicité spatiale. Les principales symétries sont :
Tab. 2-1 Principales symétries cristallines
| parallélépipèdes rectangles | |
| cubique | 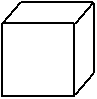 |
| tétragonale ou quadratique (base carrée) |
 |
| orthorhombique (base rectangulaire) |
 |
| prismes droits | |
| hexagonale (base losange à 120o) |
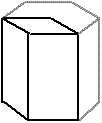 |
| monoclinique (base parallélogramme quelconque) |
 |
| prismes obliques | |
| rhomboédrique ou trigonale (tous les côtés sont égaux, tous les angles sont égaux) |
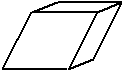 |
| triclinique (prisme quelconque) |
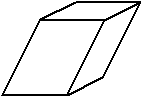 |
On voit que l'on peut découper le réseau en mailles, une maille étant la plus petite portion du réseau ayant les mêmes symétries que le réseau lui-même. Une maille est donc un prisme composée de plusieurs noeuds ; le réseau est un empilement de mailles élémentaires.
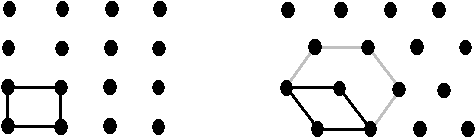
Fig. 2-4 Exemple de mailles élémentaires
dans des réseaux à deux dimensions
NB : dans le cas de la structure hexagonale, la maille de base est bien un prisme à base losange, mais du fait de sa répétition dans l'espace, on peut aussi tracer un prisme à base hexagonale, que l'on représente en grisé pour faciliter la compréhension.
Les motifs sont donc situés aux noeuds du réseau, c'est à dire aux 8 sommets de la maille élémentaire. Cependant, on a parfois des motifs situés au centre de la maille -- structure dite "centrée" -- ou bien encore aux centres des faces -- structure dite "à faces centrées".
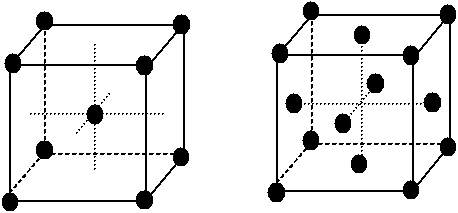
Fig. 2-5 Structures cubique centrée (cc - ou body centered cubic bcc)
et cubique à faces centrées (cfc - ou face centered cubic fcc)
En combinant ces différentes possibilités, on obtient les 14 réseaux de Bravais (cf. 3.1).
NB : les nuages atomiques étant quasiment indéformables, les cristaux monoatomiques devraient plutôt se représenter comme des boules empilées (modèle des sphères dures). Cependant, pour des raisons de clarté, on les représente comme des petites billes reliées par des barres matérialisant la maille. Dans le cas des cristaux moléculaires, il faut s'imaginer qu'il y a une molécule à chaque point noir.
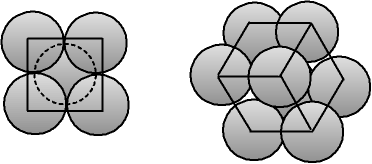
Fig. 2-6 Modèle des sphères dures pour une structure cubique centrée,
vue perpendiculaire à une face et selon une grande diagonale
Vous pouvez voir également la page sur les réseaux cristallins de l'Université du Maine (Le Mans, France), avec des animations interactives en Java.
Notes