Fig. 2-1 Analogie entre la fluorescence X et la cloche
| précédent |
| Introduction | * | Les effets de matrice | Les spectromètres | Mise en équation des effets de matrice | Bibliographie et liens |
2 -- Principes physiques
Le principe de l'analyse est le suivant : on excite l'échantillon avec un rayonnement standard (sollicitation), et on analyse le rayonnement propre réémis par l'échantillon.
Le principe est semblable à celui de la cloche : on frappe sur une cloche avec un marteau (sollicitation), et l'on récupère une note, dont la la hauteur et le timbre sont caractéristique de la cloche. Si l'on frappe plus ou moins fort, ou si l'on change de marteau, on aura toujours la même note avec le même timbre. Cependant, si l'on veut comparer les cloches entre elles, il faut que la sollicitation soit la même.

Fig. 2-1 Analogie entre la fluorescence X et la cloche
Pour la fluorescence X, on sollicite avec un rayonnement X dit «blanc» (c.-à-d. à spectre large), et l'échantillon émet des rayons X selon un spectre caractéristique.
| début |
Les rayons X sont des ondes électromagnétiques (OEM), de même nature que les ondes radio, la lumière ou les micro-ondes. Ce sont des perturbation des champs électrique et magnétique ambiants qui se propagent. Ces ondes sont en fait découpées en petits paquet d'onde, appelés photons.
Ce qui différentie les différente ondes électromagnétiques, c'est leur gamme de fréquence ou de longueur d'onde, ainsi que l'énergie que transporte chaque photon (les deux sont liés1). Les domaines des différentes ondes électromagnétiques sont représentés sur le schéma ci-dessous.
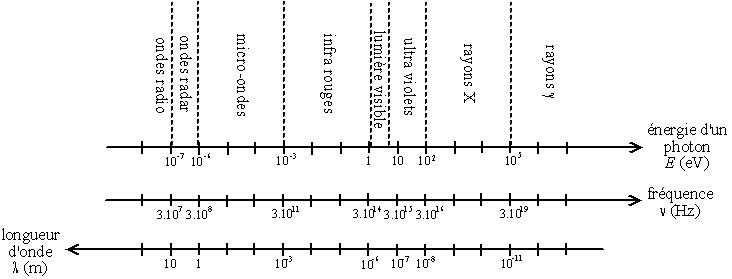
Fig. 2-2 Spectre des ondes électromagnétiques
On voit que :
Les rayons X ont été découverts en 1895 par Wilhelm Röntgen, un physicien allemand. Ils sont surtout connus pour leur pouvoir pénétrant, caractéristique utilisée en imagerie médicale pour les radiographies et les tomographies (scanners). Mais c'est ici leurs propriétés d'interaction avec les atomes qui nous intéressent.
Pour produire des rayons X, on utilise en général un tube de Coolidge : le rayonnement est provoqué par le freinage d'électrons, on parle de «rayonnement continu de freinage» ou Bremsstrahlung en allemand (c'est le terme international).
On utilise aussi parfois une source radioactive (pour les appareils portables), mais ceci tend à disparaître avec le développement de mini-tubes.
Notes
| début |
Les rayons X issus du tube excitent les atomes de l'échantillon, ils leur transmettent de l'énergie. L'état de l'atome ainsi excité est instable, l'atome va évacuer cette énergie en réémettant un photon X.
Dans un atome, les électrons sont répartis dans des couches. Plus la couche est proche du noyau, plus l'énergie de liaison noyau-électron est forte.
Du fait de leur énergie importante, les photons X vont arracher des électrons situés au coeur des atomes, près du noyau ; l'atome se retrouve ionisé.
L'ionisation de la matière par des photons porte le nom d'«effet photoélectrique», et a été découvert par Heinrich Hertz en 1887.
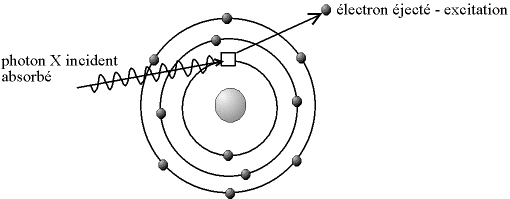
Fig. 2-3 Ionisation par effet photoélectrique
Un électron d'une couche périphérique va redescendre pour combler la place laissée vide par l'électron qui a été éjecté. Ce faisant, l'électron va perdre de l'énergie, qui va être émise sous la forme d'un photon. L'énergie de ce photon, qui est aussi dans le domaine X, est égale à la différence d'énergie entre la couche périphérique et la couche au coeur, donc chaque atome va émettre des photons d'une énergie propre. C'est le phénomène de «fluorescence», ou d'«émission caractéristique».
Il peut y avoir plusieurs transitions électroniques possibles, donc un type d'atome (un élément chimique donné) peut émettre plusieurs types de photons. Pour nommer ces différents types de photons, on utilise la notation inventée par Karl Siegbahn en 1927. Ainsi, on parle de photon Kα1, Kα2, Kβ1, Kβ2, Lα1...
Comme il s'agit d'un rayonnement électromagnétique, de radiation, on parle aussi de «raie» (line) : on a donc la raie Kα1 de l'aluminium...
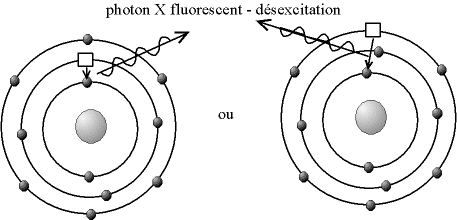
Fig. 2-4 Désexcitation par émission fluorescente
Nous avons utilisé ici la représentation de l'atome faite par Niels Bohr en 1913. Cette représentation est fausse, notamment, nous savons que les électrons ne sont pas des petites billes tournant autour du noyau, mais cette représentation est simple et suffit amplement pour expliquer les phénomènes.
| début |
Pour pouvoir analyser le rayonnement fluorescent, il faut pouvoir compter le nombre de photons de chaque type émis. On pourra ainsi représenter le nombre de photons en fonction de leur énergie, ce que l'on appelle le «spectre».
Il faut donc d'abord séparer les différents photons.
La première méthode consiste à regarder l'énergie d'un photon détecté, pour pouvoir dire dans quelle catégorie il rentre. On parle d'EDS (energy dispersive spectroscopy) ou d'EDX ou EDXRF (energy dispersive X-ray fluorescence spectroscopy).
On dispose pour cela d'un détecteur semi-conducteur (ou «détecteur solide»), en général du silicium dopé au lithium Si(Li). Ce détecteur est soumis à une tension de prépolarisation. Lorsqu'un photon X pénètre dans le détecteur, il engendre des défauts (paires électron/trou) qui permettent le passage d'un courant électrique. Ce courant est une impulsion électrique.
Plus un photon a de l'énergie, plus il crée des défauts dans le Si(Li), donc plus l'impulsion générée sera forte. La hauteur de l'impulsion est proportionnelle à l'énergie du photon, on peut ainsi immédiatement savoir de quel photon il s'agit. Après, il suffit de compter le nombre d'impulsion d'une hauteur donnée pour savoir le nombre de photon d'une énergie que le détecteur a reçu.
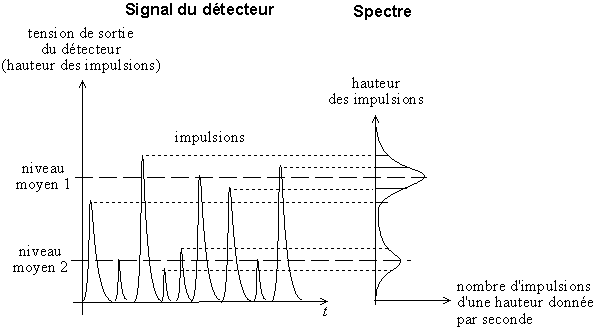
Fig. 2-5 Sélection des photons X par la hauteur des impulsions
qu'ils produisent
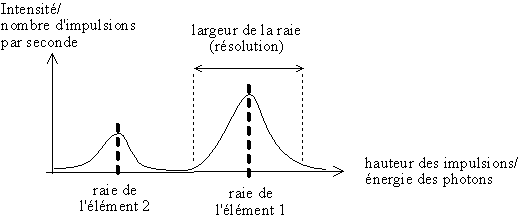
Fig. 2-6 Spectre en énergie obtenu par EDS
Pour être efficace, le système doit être maintenu froid, en général par de l'azote liquide ou bien par effet Peltier.
Le principe de la dispersion en énergie date de la fin des années 1960.
En fait, le système détecteur-préamplificateur se comporte comme un condensateur qui se charge : l'arrivé de chaque photon provoque une augmentation de la charge du condensateur, donc la tension de sortie présente une marche, la hauteur de cette marche étant proportionnelle à l'énergie du photon. On remet régulièrement à zéro cette tension. Il existe aussi des systèmes pour lesquels la tension décroît de manière exponentielle (condensateur avec résistance de fuite), ce qui évite d'avoir à remettre à zéro. Dans la suite de l'exposé, nous considérerons qu'il s'agit d'un condensateur à remise à 0 régulière.
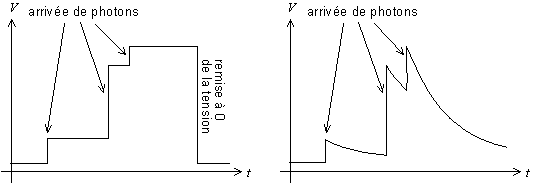
Fig. 2-7 Signal de sortie du détecteur en escalier,
avec remise à 0 régulière (gauche)
ou décroissance exponentielle (droite)
Ce signal en escalier est filtré, lissé (pour éliminer les parasites), puis on en fait la dérivée ; chaque marche devient ainsi une impulsion dont la hauteur est proportionnelle à la hauteur de la marche, donc à l'énergie du photon. Ce traitement donne le signal représenté sur la figure 2-5.
Auparavant, le filtrage et la dérivation étaient analogiques. Maintenant, on acquiert un signal numérique, que l'on traite de manière informatique. On fait un double filtrage : d'abord un filtrage de la tension, en remplaçant chaque point par la moyenne de n points (le point lui-même et les n-1 points précédents). Puis, on filtre la dérivée : celle-ci n'est pas calculée par la pente entre de deux points voisins, mais par la pente δV entre deux points séparés de 2n+g points. n et g sont deux entiers qui sont les paramètres du filtre ; n correspond en gros au temps minimal séparant deux marches, et g à la durée de transition entre le bas et le haut de la marche (gap). Ce filtrage donne des impulsions en forme de trapèze. Le temps de montée (rise time) et la durée du plateau (flat top time) du trapèze dépendent respectivement de n et de g.
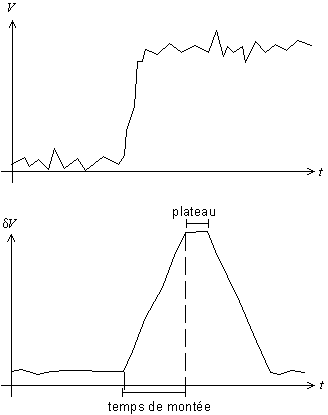
Fig. 2-8 Double filtrage numérique
de la courbe dérivée :
impulsion trapézoïdale
Si l'on effectue un filtrage important (n grand), on élimine les fluctuations aléatoires du signal, donc on peut détecter de plus petites marches, les pics du spectre en énergie sont plus étroits (meilleure résolution en énergie) ; par contre, les impulsions sont plus larges, on risque donc de ne pas compter des photons si les impulsions se recouvrent (problème de l'empilement ou pile up). Si l'on filtre peu (n petit), on réduit le risque d'empilement, donc on peut travailler avec des arrivées de photons plus rapprochées (intensité importantes) ; par contre, le bruit est plus important, donc les pics du spectre en énergie sont plus larges (perte de résolution).
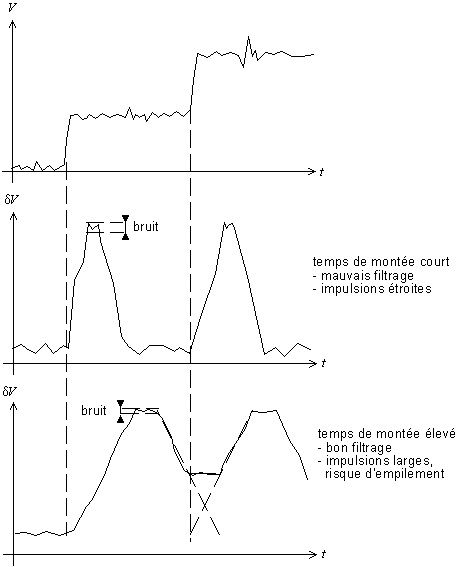
Fig. 2-9 Signal de sortie (haut)
traité avec deux paramètres de filtrage différents ;
l'amélioration de la résolution
augmente le risque d'empilement des impulsions
NB
on pourrait s'attendre à ce que les impulsions soient centrées
sur le point d'inflection de la marche.
Ici, c'est le pied de l'impulsion qui se trouve au point d'inflection :
c'est un artefact de l'algorithme,
la dérivée doublement filtrée δV
est calculée en temps réel,
donc le point calculé à l'instant t
correspond en fait à l'instant t-n-g/2
(milieu de l'intervalle servant à calculer la pente).
Ce décalage temporel n'a absolument aucune influence sur le résultat.
La seconde méthode consiste à séparer les photons avant de les compter, un peu comme on sépare les couleurs de la lumière avec une flaque d'huile (irisation). On parle de WDS (wavelength dispersive spectroscopy), ou de WDX ou WDXRF (wavelength dispersive X-ray fluorescence spectroscopy).
On utilise pour cela la diffraction sur des cristaux.
Si l'on regarde une flaque d'huile, on constate des irisations. Il s'agit d'une décomposition de la lumière, qui est possible car l'épaisseur de la couche d'huile est de l'ordre de grandeur de la longueur d'onde de la lumière. De même, les rayons X vont être décomposés (diffractés) par les couches atomiques d'un cristal, puisque l'épaisseur d'une couche atomique (la distance interatomique) est de l'ordre de grandeur de la longueur d'onde des rayons X.
Ce principe a été découvert par Max von Laue en 1912, et a été développé par W.H. et W.L. Bragg en 1915.
Il suffit alors de placer le détecteur (ou compteur) dans la bonne direction pour compter les photons d'une longueur d'onde (donc d'une énergie) donnée. On se repère par l'angle de déviation 2θ des photons2 ; on peut calculer l'énergie d'un photon en fonction de son angle de déviation.
Ainsi, en traçant l'intensité (nombre d'impulsions par seconde détectées à une position donnée) en fonction de la position 2θ du détecteur, on obtient le spectre en énergie (l'échelle des énergies est inversée par rapport à celle des angles3).
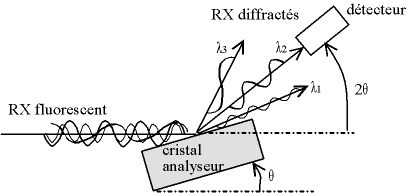
Fig. 2-10 Sélection des photons X par diffraction sur un cristal
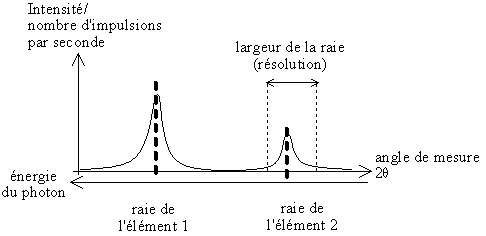
Fig. 2-11 Spectre en énergie inversé,
obtenu par WDS
Notes
2.d.sin(θ) = n.λ
où n est un entier appelé ordre de diffraction,
et θ est la moitié de l'angle de déviation
retour
E = h.c/(2.sin(θ))
retour