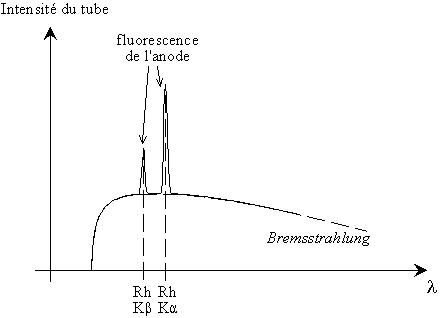
Fig. 5-1 Spectre d'émission d'un tube à rayons X (tube de Coolidge)
| précédent |
| Introduction | Principes physiques | Les effets de matrice | Les spectromètres | * | Bibliographie et liens |
5 -- Mise en équation des effets de matrice
Les effets de matrice ont été mis en équation par J. Sherman en 1955 (une erreur a été corrigée par T. Shiraiwa et N. Fujino en 1966), la première approche des corrections de matrice par les paramètres fondamentaux fut faite par J.W. Criss et L.S. Birks en 1968. Nous ne présenterons pas ici l'équation en elle-même, mais d'une part les équations de base de l'absorption ayant servi à l'établir, et d'autre part une version globale simplifiée de l'équation.
Les lois physiques sont établies pour une longueur d'onde donnée. En spectrométrie de fluorescence X, on excite avec un rayonnement polychromatique, il faut donc commencer par connaître le spectre d'émission du tube pour pouvoir intégrer les lois sur toutes les longueurs d'ondes disponibles.
Les rayons X sont produits par le freinage des électrons (Bremsstrahlung, en allemand bremmen "freiner", et die Strahlung "la radiation"). Comme le freinage est aléatoire, on a un spectre continu (ou «blanc»). L'énergie maximale pour un photon (c.-à-d. la longueur d'onde minimale) correspond à un électron stoppé net, c'est donc l'énergie cinétique des électrons incidents.
À ce fond continu s'ajoute la fluorescence interne de l'anode du tube à rayons X, en général en rhodium Rh.

Fig. 5-1 Spectre d'émission d'un tube à rayons X
(tube de Coolidge)
La première mesure d'un spectre de tube a été faite par A. Jönnson (physicien suédois) en 1927.
| début |
L'absorption suit une loi de Beer-Lambert :
I(x) = I0.exp(-μ.ρ.x)où I0 est l'intensité des rayons X lors de l'entrée dans la matière, I(x) est l'intensité des rayons X après avoir parcouru une distance x dans la matière, μ(λ) est le coefficient d'absorption massique qui dépend de la longueur d'onde λ des rayons X et de la nature chimique de la matière, et ρ est la densité de la matière.
Pour un élément chimique donné, μ(λ) suit une loi en dents de scie, les sauts d'absorption (absorption edge) correspondant aux énergies d'ionisation.
Les valeurs de μ sont tabulées pour tous les éléments et une large gamme de longueurs d'onde ; pour un échantillon composite, il suffit d'appliquer une loi de composition des masses.
L'absorption des rayons X par la matrice joue :
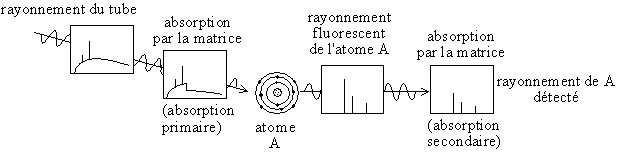
Fig. 5-2 Modification du spectre fluorescent en raison de
l'absorption par la matrice
| début |
On va supposer que notre échantillon contient de l'aluminium Al avec une concentration cAl, que l'on excite l'échantillon avec un faisceau X monochromatique d'énergie E et que l'on s'intéresse à la raie Kα de l'aluminium (dont les photons ont une énergie EAl Kα).
Les photons X venant du tube peuvent être capturés ou bien passer à côté d'un atome Al. Il y a ce que l'on appelle la «section efficace» σ(E), la probabilité d'interaction est le produit de la section efficace et de la concentration d'atomes Al : σ(E).cAl.
Si le photon et l'atome Al interagissent, cela peut se faire de plusieurs manières :
Si l'atome est ionisé par effet photoélectrique, l'électron qui est arraché peut provenir de n'importe quelle couche. Par ailleurs, l'électron qui vient combler la place vacante peut provenir de n'importe quelle couche supérieure (dans la limite des transitions possibles). Donc, il n'y a qu'une probabilité pKα que la transition Kα ait lieu. Ensuite, si la transition a lieue, elle va libérer son énergie :
Au total, pour un petit volume dV situé au coeur de la matière, l'intensité d3IAl Kα de la raie Al Kα est :
d3IAl Kα = I0(E).β1(E).cAl.σ(E).FAl Kα.β2(EAl Kα).dVoù I0(E) est l'intensité des rayons X incidents, β1(E) est l'absorption primaire (cela dépend de la composition de l'échantillon et du chemin parcouru), FAl Kα est la probabilité pour l'atome d'émettre un photon Kα en se désexcitant (F regroupe entre autres p, r et ω), et β2(EAl Kα) est l'absorption secondaire. Il faut intégrer cette équation sur tout le volume (β1 et β2 changent avec la profondeur).
Nous avons ici défini la probabilité qu'un photon Al Kα frappe le détecteur, mais... pour une énergie d'excitation donnée (faisceau monochromatique). Il faut maintenant intégrer sur le spectre d'émission du tube. Et ne pas oublier que le spectre fluorescent se superpose au spectre du tube (surexcitation).
| début |
Au bout du compte, on obtient l'équation de Lachance-Traill1 :
ci = mi.Ii.(1 + Σj <> i αij.cj)où i est un élément donné, Ii est l'intensité de la raie fluorescente de i, ci est la concentration de i dans l'échantillon, mi est le coefficient d'étalonnage pour la raie de i (il s'agit de l'inverse de l'intensité mesurée sur un échantillon de i pur), les cj sont les concentrations en autres éléments, et les αij sont les coefficients inter-élément.
αij représente la manière dont l'élément j va influencer l'intensité de la raie de i, par l'absorption et la fluorescence secondaire. αij dépend lui-même de la composition de l'échantillon, donc ce n'est pas une constante.
On voit tout de suite que cette équation est "dans le mauvais sens" : elle donne l'intensité en fonction des concentrations, or, lorsque l'on fait une mesure, on a les intensités et l'on cherche les concentrations. Les algorithmes classiques procèdent donc en général comme suit :
Si l'on travaille avec une gamme d'échantillons relativement homogène, alors on peut fixer les αij pour un échantillon moyen (les αij varient en fait peu d'un échantillon à l'autre), et l'on a alors juste une matrice à inverser pour avoir les concentrations.
| début |
À l'époque où l'on ne disposait pas de toutes les valeurs tabulées et de la puissance de calcul nécessaire pour prendre en compte les effets de matrice avec les paramètres fondamentaux, il a fallu mettre en place des méthodes empiriques.
La première méthode a consisté à considérer, pour une gamme d'étalonnage donnée, que les α étaient constants, et à les déterminer par régression.
Cette méthode donne de bons résultats à condition que les variations de concentrations soient modérées (hypothèse des α constants), mais présente un inconvénient de taille... le nombre d'étalons nécessaires pour déterminer les α.
En effet, si l'on a n éléments présents dans l'échantillon, il faut déterminer n coefficients mi, et n.(n-1) coefficients αij. Il faut donc au minimum n2 étalons, et encore faut-il les prendre avec des proportions variables deux à deux.
La notion d'étalon interne est très répandue en analyse chimique. Elle consiste à ajouter une quantité connue d'un produit ; si les effets de matrice sont les mêmes sur l'étalon interne que sur les éléments à mesurer, alors le rapport des intensités Iélément/Iétalon interne sera proportionnel à la concentration en élément,
ci = mi.Ii/Iétalon interne.De manière générale, ceci est faux en fluorescence X, car l'absorption dépend de l'énergie de la raie, la surexcitation dépend des énergies de liaison des électrons aux atomes, donc l'élément mesuré ne subit pas les mêmes effets de matrice que l'étalon interne. C'est toutefois acceptable si la raie de l'étalon interne et celle de l'élément analysé sont proches en énergie ; alors, elles subissent une absorption similaire, et l'on peut espérer que la surexcitation soit aussi comparable.
Notons que la méthode n'est possible que sur des échantillons liquides, puisqu'il faut pouvoir ajouter un produit de manière homogène ; dans le cas de solides, certaines personnes utilisaient la raie Compton (c.-à-d. la raie Kα du rhodium de l'anode du tube qui est diffusée de manière inélastique par l'échantillon). On n'a alors pas à proprement parler d'étalon interne, disons que l'on se sert, comme référence, de la réflexion du spectre du tube sur l'échantillon.
Tous ces inconvénients font que cette méthode est quasiment abandonnée, à l'exception d'un cas particulier : la mesure du soufre S dans les essences, fuels, diesels et huiles. Dans ce cas, on a :
| début |
Les interactions électromagnétiques se font par quanta (les photons), durant l'interaction, l'énergie est concentrée dans un paquet d'onde ; cette loi relie le quantum d'énergie à la longueur d'onde λ de l'onde électromagnétique
E = h.c/λh = 6,6.10-34 J.s est la constante de Planck et c = 3.108 m/s est la vitesse de la lumière dans le vide
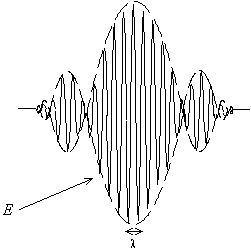
Fig. 5-3 Le photon,
un paquet d'onde contenant une énergie E
Manne Sigbahn a proposé, en 1924, une notation pour désigner les sauts électroniques qui provoquaient l'émission de photons X. Une raie est due à une transition d'un niveau de départ vers un niveau d'arrivée (celui laissé vacant par l'électron éjecté par effet photoélectrique).
| Niveau d'origine de l'électron | Niveau d'arrivée de l'électron | Nom de la raie (Siegbahn) |
|---|---|---|
| L3 (2P3/2) | K (1S0) | Kα1 |
| L2 (2P1/2) | K (1S0) | Kα2 |
| M3 (3P3/2) | K (1S0) | Kβ1 |
| M5 (3D5/2) | L3 (2P3/2) | Lα1 |
| M4 (3D3/2) | L2 (2P1/2) | Lβ1 | N7 (5P3/2) | M5 (3D5/2) | Mα1 |
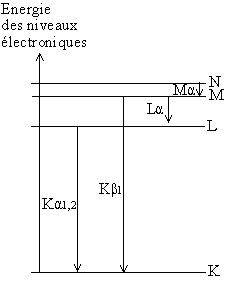
Fig. 5-4 Raies spectrales
- transitions électroniques et notation de Siegbahn
Relie la longueur d'onde λ d'une raie avec le numéro atomique Z de l'élément
1/λ = K.(Z - σ)2K et σ sont des constantes qui dépendent du type de raie (il y a un couple de constantes pour les raies Kα, un autre pour les raies Kβ, Lα...) ; σ est une constante d'écran qui est légèrement inférieure à 1
Relie l'angle de déviation 2θ à la longueur d'onde λ des rayons X lors de la diffraction sur un cristal de distance interréticulaire d
2.d.sin(θ) = n.λoù n est un entier (ordre de diffraction, on ne considère en général que l'ordre n = 1) et θ est la moitié de la déviation
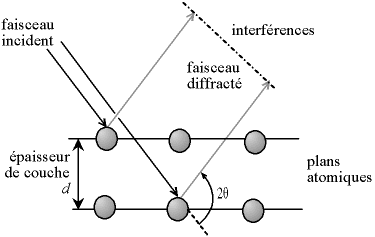
Fig. 5-5 Loi de Bragg
donnant les angles de diffraction des rayons X sur un cristal
C'est une loi générale d'absorption, initialement utilisée pour l'absorption de la lumière. L'intensité I de l'onde électromagnétique (c.-à-d. le flux énergie par unité de surface et de temps) diminue lorsqu'elle traverse une épaisseur d de matière, elle est absorbée selon la loi :
I(d) = I0.exp(-μL.d)où μL est le coefficient linéaire d'absorption, qui dépend de la longueur d'onde λ, et I0 est l'intensité de l'onde avant d'entrer dans la matière. Dans le cas des rayons X, μL est proportionnel à la densité, on écrit donc
μL = μ.ρoù μ est le coefficient d'absorption massique et ρ est la masse volumique.
et
I(d) = I0.exp(-μ.ρ.d)
Si le faisceau incident pénètre avec un angle ψ1 dans l'échantillon et provoque la fluorescence Kα d'un atome Al situé à une profondeur e, alors, le chemin d1 qu'il aura parcouru dans la matière est
d1 = e/sin(ψ1)le rayon fluorescent qui se dirige vers le détecteur fait un angle ψ2 avec la surface, il parcours donc un chemin d2 dans la matière
d2 = e/sin(ψ2)les facteurs d'absorption primaires et secondaires pour cet atome sont donc
exp(e.μ(E)/sin(ψ1))en intégrant ces facteurs sur l'épaisseur, on trouve les facteurs d'absorption totaux β.
et
exp(e.μ(EAl Kα)/sin(ψ2))
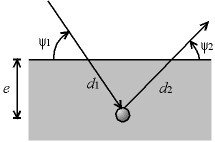
Fig. 5-6 Chemin parcouru par les rayons X dans la matière
On peut définir le coefficient d'absorption massique μi(λ) pour un élément pur i (par exemple, μAl(λ) est le cofficient d'absorption massique pour un échantillon d'aluminium pur). Si un matériau est composé de plusieurs éléments i, avec les concentrations massiques ci, alors le coefficient d'absorption massique total μ du matériau est :
μ(λ) = Σ ci.μi(λ)NB : il faut bien utiliser le coefficient d'absorption massique et non pas le coefficient d'absorption linéaire.
Relie, entre deux discontinuités d'absorption, le coefficient d'absorption massique μ à la longueur d'onde λ du rayonnement et au numéro atomique Z de l'élément absorbant
μ(λ) = k.Z4.λ3k est une constante qui change à chaque discontinuité.
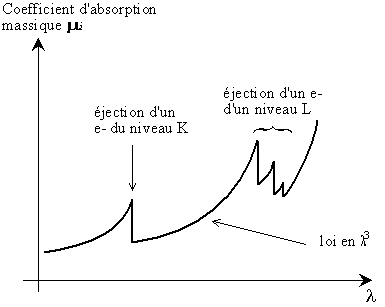
Fig. 5-7 Variation de l'absorption delon la longueur d'onde
pour un élément donné
Relie le rendement de fluorescence ω au numéro atomique Z de l'élément
ω = Z4/(Z4 + c)où c est une constante qui dépende du type de raie, (c = 105 pour les raies K, 109 pour les raies M)
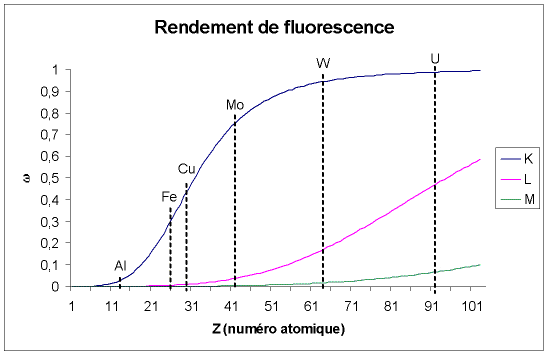
Fig. 5-8 Rendement de fluorescence ω
en fonction du numéro atomique Z
pour trois séries de raies