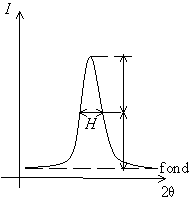
Fig. 7-1 Largeur à mi-hauteur
| Introduction | Méthodes de mesure | Recherche de phases | Principes physiques | Décalages | Surface | * | Intensité | Profil | Biblio |
| précédent |
La position en 2θ d'un pic est imposée par la structure cristallographique. La surface nette du pic est imposée par la proportion de phase dans l'échantillon, l'absorption des rayons X par l'échantillon, et l'orientation des cristallites.
Mais pour une surface donnée, un pic peut être plus ou moins large (étalé), donc plus ou moins haut. On caractérise la largeur d'un pic par sa largeur à mi-hauteur H (en anglais full width at half maximum FWHM), c.-à-d. la largeur du pic à mi-chemin entre la ligne de fond continue et le sommet du pic.

Fig. 7-1 Largeur à mi-hauteur
H est déterminé par deux paramètres de l'échantillon : les microcontraintes résiduelles et la taille des cristallites.
On a vu que lorsque des contraintes déforment la maille, cela produit un décalage du pic. Si maintenant chaque cristallite est soumis à une contrainte différente, on a alors une juxtaposition de pics voisins qui se superposent. C'est ce que l'on appelle les «microcontraintes»
On a donc une répartition de contraintes. On peut souvent modéliser cette répartition par une statistique normale, c.-à-d. une loi gaussienne. Par rapport à un échantillon sans contrainte, on a une augmentation Hg de la largeur à mi-hauteur qui vaut
Hg = 5.e.tan(θ)où e est la moyenne quadratique des déformation Δd/d, d étant la distance interréticulaire normale (cette formule donne Hg en radians, attention à la conversion en degrés). On voit que cet élargissement augmente avec l'angle de diffraction 2θ.
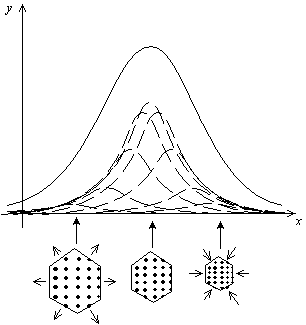
Fig. 7-2 Largeur du pic : effet des microcontraintes,
juxtaposition de plusieurs pics
| début |
Plus les cristallites sont petits, plus les pics sont larges. Cet effet devient visible pour les cristallites faisant moins de 1 μm de diamètre. Ceci s'explique de la manière suivante.
Lorsque l'on est en condition de Bragg pour un plan (hkl) (c.-à-d. 2θ = 2θhkl), les rayons diffractés par deux plans atomiques successifs sont en phase, donc les intensités s'additionnent. Supposons que nous nous écartons maintenant légèrement des conditions de Bragg (2θ = 2θhkl+ε), il n'y a alors qu'un léger déphasage α(1) entre les rayons diffractés par deux plans successifs, donc les intensités s'additionnent également. En fait, le rayon diffracté par le premier plan atomique sera annulé par le premier rayons en opposition de phase, donc le rayon diffracté par le plan m = π/α.
S'il y a moins de m plans dans le cristallite, alors l'intensité ne sera pas nulle pour cet angle de diffraction 2θhkl+ε. Ce sera le cas si le cristallite est plus petit que m.d (d étant la distance interréticulaire des plans (hkl)).
Donc, par rapport à un pic mesuré sur un échantillon à gros cristallites, on un élargissement du pic Hl qui est donné par la formule de Scherrer (1918) :
Hl = k.λ/(τ.cos(θ))où k est un facteur de forme qui vaut
Il faut bien se poser la question de la signification de la valeur trouvée. En effet, les cristallites n'ont pas une taille unique, il y a une distribution de tailles. Dans le cas d'une distribution dite « unimodale » (c'est-à-dire avec un seul maximum), il faudrait au minimum trois informations :
La valeur trouvée reflète la « hauteur des colonnes atomiques ». Il s'agit en fait de la moyenne volumique de ces hauteurs Lvol, c'est-à-dire que l'on pondère la hauteur de chaque colonne par le volume de la colonne pour en faire la moyenne.
Dans le cas où les cristallites ont des formes anisotropes, par exemple allongée sous forme d'aiguilles ou d'assiettes, alors la hauteur de colonne varie selon l'orientation cristallographique, donc les pics d'une même phase n'ont pas tous la même largeur. Ainsi, la formule de Scherrer peut nous renseigner sur la forme des cristallites. Pour des assiettes de type « cylindre plat », le pic correspondant aux colonnes dans l'axe du cylindre donnerait l'épaisseur moyenne des assiettes, et le pic correspondant aux colonnes parallèles à la base correspondant aux diamètre moyen des assiettes (avec un coefficient 4/3). Mais il faut faire attention aux conditions de préparation : si toutes les assiettes s'empilent, on aura de l'orientation préférentielle.
Par ailleurs, il faut faire attention au fait que l'on peut caractériser la « position » d'une statistique par son maximum, sa moyenne volumique, sa moyenne massique, sa moyenne particulaire, sa médiane… Dans le cas typique d'une distribution unimodale, celle-ci est dissymétrique (on peut avoir des cristallites très grands, mais pas de volume nul) ; la formule de Scherrer donnant la moyenne volumique, celle-ci est en plus élevé que le maximum de la statistique et que tous les autres paramètre cités ci-dessus.
| début |
Si l'on mesure un pic sur un échantillon sans microcontrainte et ayant une taille de grain supérieure à 1 μm, on obtient une largeur à mi-hauteur H0, que l'on appelle «largeur instrumentale». Sur un échantillon quelconque, la largeur du pic vaut
H = H0+Hg+HlLa largeur instrumentale varie elle-même en fonction de la position du pic 2θ (on peut la calculer, cf. la page profil du pic), mais si on fait l'approximation qu'elle est constante, alors la largeur des pics pour une phase donnée évolue selon
H = A+B.tan(θ)+C/cos(θ)A, B et C étant des constantes. Les pics de deux phases différentes peuvent donc avoir des largeurs différentes.
Certaines personnes utilisent la loi de Cagliotti3 pour décrire la dépendance angulaire de la largeur de pic :
H2 = U.tan2(θ)+V.tan(θ)+Wcette loi fut établie sur des expérience de diffraction de neutrons, elle fut beaucoup utilisée comme loi empirique, elle est maintenant tombée en désuétude dans le domaine de la diffraction X.
Notes
retour
retour
retour