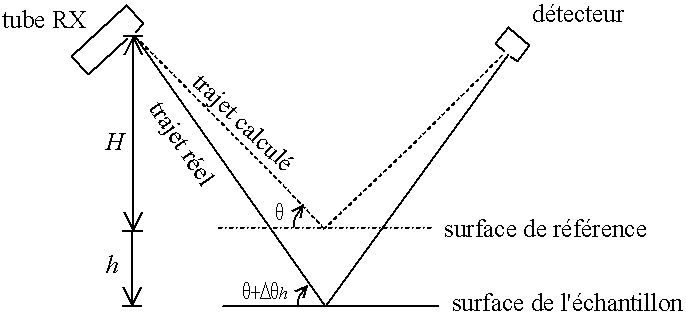
Fig. 5-1 Ecart sur la position du pic lorsque l'échantillon n'est pas à la bonne hauteur
| Introduction | Méthodes de mesure | Recherche de phases | Principes physiques | * | Surface des pics | Largeur | Intensité | Profil | Biblio |
| précédent |
Le décalage des pics par rapport à la position théorique (de la signature) peut créer des problèmes pour l'identification des phases, mais cela peut aussi être une source d'informations sur les caractéristiques physiques de l'échantillon.
La première source de décalage possible est un mauvais réglage de l'appareil. Il faut donc ajuster avec précision le zéro du goniomètre. Les appareils actuels sont stables et n'ont besoin d'être réglés que lorsque l'on modifie le dispositif (p.ex. changement de pièces, modification de la configuration, ajout d'accessoires).
Si le goniomètre est mal réglé, cela se traduit par un décalage uniforme, c.-à-d. que tous les pics de toutes les phases sont décalés de la même quantité, d'un bout à l'autre du diffractogramme.
| début |
Lorsque l'on a un diffractomètre de Bragg-Brentano, la surface de l'échantillon doit se trouver à un niveau précis. Si cette surface se trouve au-dessus ou en-dessous, alors, l'angle de déviation 2θ du faisceau diffère de l'angle calcué par l'appareil à partir de la position du tube et du détecteur (dans le cas d'un θ-θ, à partir de la position du porte-échantillon et du détecteur dans le cas d'un θ-2θ).

Fig. 5-1 Ecart sur la position du pic
lorsque l'échantillon n'est pas à la bonne hauteur
Les pics seront décalés d'une valeur Δ2θ par rapport à leur position attendue, et cet écart varie en fonction de l'angle de déviation lui-même :
Δ2θ = -2.cos(θ).h/Roù h est l'erreur de hauteur et R est le rayon du goniomètre.
Si l'acquisition se fait entre 0 et 70 ° (pour 2θ), cos(θ) passe de 1 à 0,82, donc le décalage sera quasiment le même sur tout le diffractogramme, il sera difficile de distinguer s'il s'agit d'un problème de goniomètre ou un problème de hauteur d'échantillon.
| début |
Les contraintes, ce sont les forces internes à la matière. Si ces forces induisent des déformations de la maille cristalline (déformation élastique), elles vont faire varier les distances interréticulaires d, et donc décaler la position des pics. Si l'on mesure le décalage des pics, on peut donc en déduire l'état de contrainte de l'échantillon.
Les contraintes internes peuvent être source d'imperfection, de dégradation des pièces mécaniques, c'est la raison pour laquelle elles sont beaucoup étudiées en métallurgie.
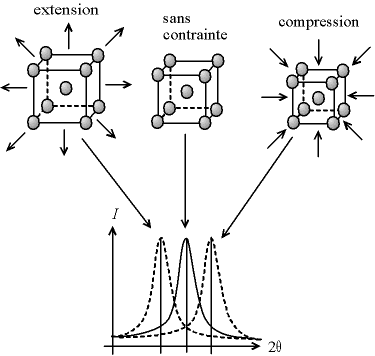
Fig. 5-2 Ecart sur la position du pic
dû à une contrainte
N.B. : la section suivante ne concerne que les diffractomètres à détecteur mobile, pas les chambres de Debye-Scherrer.
Ainsi, en mesurant la position du pic, on peut en déduire la déformation de la maille, et si l'on connaît les coefficients d'élasticité on peut calculer la valeur de la contrainte.
Cependant, les plans diffractants sont les plans parallèles à la surface de l'échantillon. On ne peut donc mesurer que les contraintes perpendiculaires à la surface, donc
On peut incliner l'échantillon latéralement (tilt), autour de l'axe qui est l'intersection du plan du faisceau (plan contenant les faisceaux incident et diffracté) et la surface de l'échantillon, d'un angle χ. On parle de «montage chi» (prononcer "ki") ; ceci permet d'avoir la plus grande amplitude de mesure (χ varie de 0 à 90 ° en théorie, dans la pratique, l'intensité est trop faible vers 90 °), mais nécessite un montage spécial, appelé «berceau d'Euler» ou «montage 4 cercles».
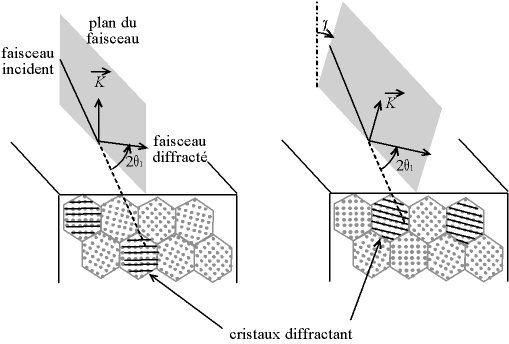
Fig. 5-3 Montage chi : inclinaison latérale,
ce ne sont pas les mêmes cristallites qui diffractent
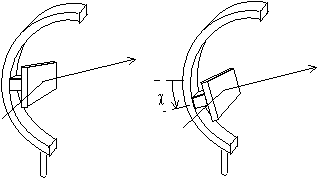
Fig. 5-4 Berceau d'Euler ou montage 4 cercles :
on peut incliner l'échantillon latéralement,
notez qu'ici le plan du faisceau est horizontal
On peut aussi incliner l'échantillon selon l'axe perpendiculaire au plan du faisceau d'un angle Ω. On parle «montage Oméga» ou de «rocking curves». Ce montage peut se faire avec un appareil classique, puisqu'Ω est en fait l'angle d'incidence des rayons X ; on est limité en angle d'inclinaison (les faisceaux incident et diffracté sont à la limite tangents à la surface), mais comme on utilise en général des déviations 2θ importantes (le décalage du pic est plus marqué aux angles élevés), on dispose d'une amplitude correcte.
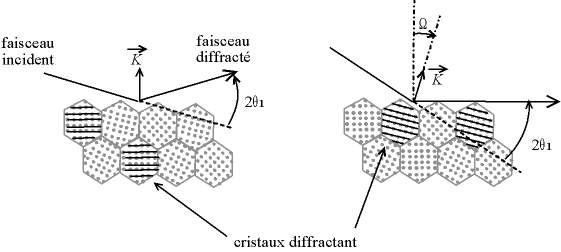
Fig. 5-5 Montage Oméga : inclinaison de l'incidence du faisceau,
ce ne sont pas les mêmes cristallites qui diffractent
Quelle que soit la méthode d'inclinaison, on fait ensuite tourner l'échantillon dans son plan (axe perpendiculaire à sa surface, spin) d'un angle φ (phi). Une fois l'échantillon dans cette position, on effectue un balayage autour du sommet du pic afin de pouvoir localiser celui-ci. On fait ceci pour plusieur valeurs de χ/Ω et de φ, ce qui permet d'avoir la "cartographie angulaire" des contraintes, et donc de calculer le tenseur des contraintes1.
| début |
Une des sujets de la cristallographie est la détermination des structures cristallines, et notamment des paramètres de maille ; mais ceci dépasse le sujet de cet article, on pourra se reporter pour plus d'informations à l'article d'Armel Le Bail (Université du Maine, Le Mans, France) intitulé Stratégies des déterminations structurales sur poudre. Cela passe notamment par une étape de simulation selon la méthode de Rietveld2 : on connaît les "coefficients de réflexion" (en fait, les facteurs de diffusion) des atomes pour les rayons X, à partir d'une structure cristallographique supposée (c.-à-d. position des atomes dans la maille), on peut simuler le diffractogramme. On compare le diffractogramme simulé avec le diffractogramme réel, et on afine les paramètres de structure afin de se rapprocher le plus possible de la courbe mesurée.
Par contre, un sujet voisin est bien plus facile à comprendre : celui de l'ajustement de structure. On connaît déjà la structure cristallographique du produit idéal, mais les paramètres de maille sont légèrement différents car la composition chimique n'est pas exactement la même. La position 2θ des pics mesurés nous donne les distances interréticulaires dhkl du cristal et donc les paramètres de maille de notre produit, on peut ainsi en déduire en quoi il est différent du produit idéal.
Une des modifications chimiques les plus courantes est la solution solide. Soit les atomes "natifs" sont remplacés par des atomes étrangers, on parle de «substitution» (si l'atome étrangers est plus gros, on a une dilatation de la maille, si il est plus petit, on a une contraction) ; soir les atomes étrangers viennent se glisser dans les interstices de la maille, on parle d'«insertion» (on a une dilatation).
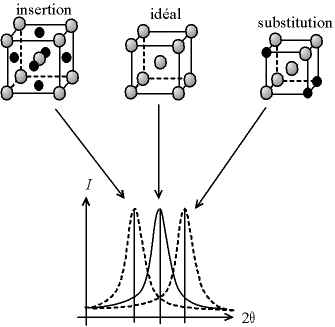
Fig. 5-6 Solution solide :
variation des paramètres de maille
Liens
Note
l'état de contrainte
est représenté par une matrice 3×3,
les coefficients étant les trois composantes du vecteur force
sur les trois faces de référence ;
selon l'orientation des faces et du repère,
les valeurs numériques changent
mais l'état de contraintes reste le même ;
le terme «tenseur» recouvre
cette notion d'objet invariant par les changements de base
(voir un cours d'élasticité pour plus de détails)
retour
retour