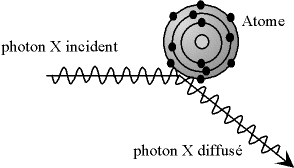
Fig. 4-1 Diffusion élastique : les photons X rebondissent en gardant la même énergie
| Introduction | Méthodes de mesure | Recherche de phases | * | Décalage de pics | Surface des pics | Largeur | Intensité | Profil | Biblio |
| précédent |
Les rayons X sont une onde électromagnétique. Les rayons X interagissent avec le nuage électronique des atomes. Parmi les interactions possibles, il y a la «diffusion élastique», ou «diffusion Rayleigh».
Dans la diffusion élastique, les rayons X rebondissent simplement sur le nuage électronique, ils sont diffusés dans toutes les directions de l'espace, en gardant la même énergie, la même longueur d'onde.

Fig. 4-1 Diffusion élastique :
les photons X rebondissent en gardant la même énergie
On peut décrire ceci de la manière suivante : les ondes électromagnétiques mettent en mouvement le nuage électronique par rapport au noyau de l'atome. Ceci crée un dipôle vibrant, qui rayonne lui-même des ondes de même fréquence à la manière d'une antenne.
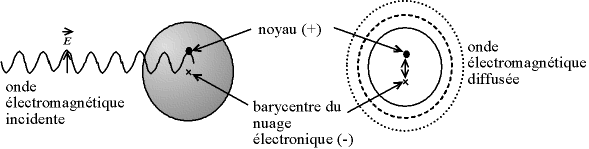
Fig. 4-2 Diffusion élastique :
modèle du dipôle vibrant
Lien
| début |
Lorsque les rayons X frappent un morceau de matière, ils sont donc diffusés par chacun des atomes de la cible. Ces rayons X diffusés interfèrent entre eux. Si les atomes sont ordonnés, c.-à-d. placés à des intervalles réguliers (ce qui caractérise les cristaux), alors ces interférences vont être constructrices dans certaines directions (c.-à-d. les ondes s'additionnent), destructrices dans d'autres (c.-à-d. les ondes s'annulent). Ces interférences d'ondes diffusées forment le phénomène de diffraction.
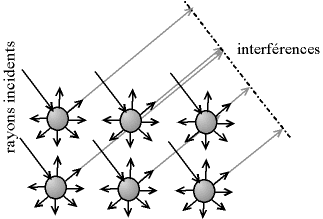
Fig. 4-3 interférence des ondes diffuées
- phénomène de diffraction
Donc, pour certains angles de déviation 2θ du faisceau, on détecte des rayons X (interférences constructrices), ce sont les pics du diffractogramme ; ces angles de déviation sont caractéristiques de l'organisation des atomes dans la maille cristalline. Dans les autres directions, on ne détecte pas de rayon X, c'est la ligne de fond du signal.
Lien
| début |
Si l'on calcule les directions dans lesquelles on a du signal, on s'aperçoit que l'on obtient une loi très simple : si l'on trace des plans imaginaires parallèles passant par les atomes, et si l'on appelle d la distance entre ces plans (ou «distance interréticulaire»), alors les interférences sont constructrices si
2.d.sin(θ) = n.λoù θ est la moitié de la déviation, n est un nombre entier appelé «ordre de diffraction», et λ est la longueur d'onde des rayons X (souvenez-vous que l'on travaille en monochromatique). Cest la loi de Bragg.
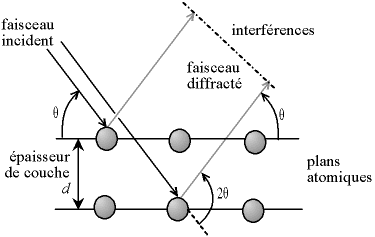
Fig. 4-4 Loi de Bragg donnant les directions
où les interférences sont constructrices
Si le faisceau de rayons X qui éclaire l'échantillon est ponctuel (ou tout du moins est un fin cylindre), il y a alors une symétrie de révolution autour de l'axe du faisceau. Les rayons diffractés forment donc des cônes dont l'axe est le faisceau incident. Dans le cas d'une chambre de Debye-Scherrer, les anneaux de Debye qui impressionnent le film sont les traces de ces cônes.
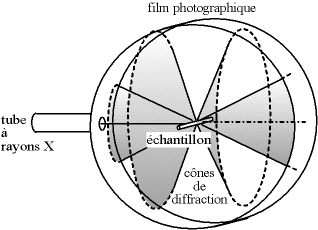
Fig. 4-5 Cônes de diffraction et anneaux de Debye
dans une chambre de Debye-Scherrer
Dans le cas d'un diffractomètre de Bragg-Brentano, le détecteur de rayons X enregistre un maximum lorsqu'il se trouve sur un cône. (Sur l'image ci-dessous, les cônes devraient bien sûr être tronqué sous l'échantillon, car les rayons X sont absorbés par l'échantillon et le porte-échantillon. J'ai volontairement négligé ce point pour des raisons de clarté.)
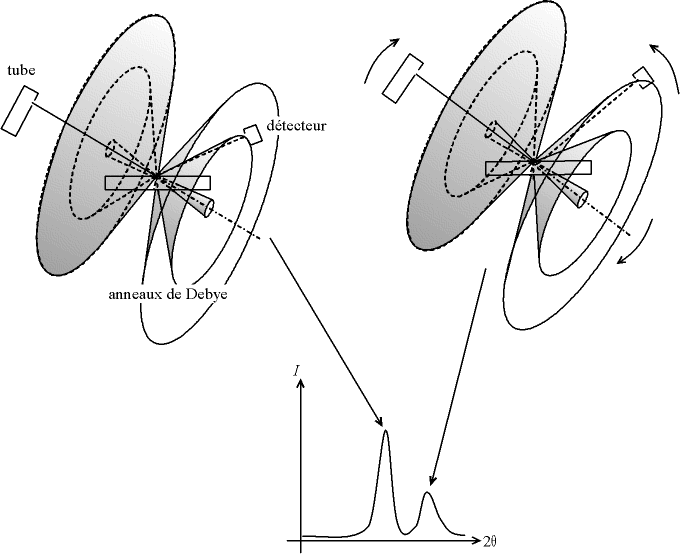
Fig. 4-6 Cônes de diffraction et signal détecté
dans un diffractomètre de Bragg-Brentano
Par la loi de Bragg, on peut donc associer chaque pic à un plan atomique imaginaire. On sait que ces plans peuvent être désignés par des indices de Miler (hkl). On peut donc de même associer ces indices (hkl) aux pics de diffraction. On parle d'«indexation des pics».
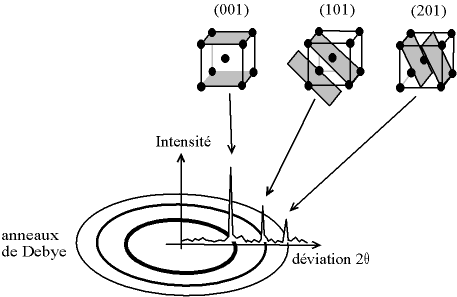
Fig. 4-7 Indexation des pics :
association d'un pic de diffraction et d'un plan (hkl)
Dans le cas d'une chambre de Debye-Scherrer, le faisceau incident est un fin cylindre, le trait qui sert à le représenter dans ce document est donc pertinent.
Dans le cas d'un diffractomètre de Bragg-Brentano, le faisceau est divergent et a une section rectangulaire (la fenêtre de sortie du tube est un rectangle d'environ 1 cm de large pour 1 mm de haut).
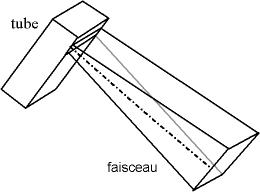
Fig. 4-8 Divergence du faisceau :
faisceau à section rectangulaire
Si l'on regarde le dispositif de profil, on considère par approximation que l'échantillon, le tube et le détecteur se trouvent sur un cercle, appelé «cercle de focalisation de Rowland», donc si le cône d'un des rayons incidents passe par le détecteur, les cônes des autres rayons aussi. On peut donc assimiler tous ces rayons au rayons central, et donc représenter le faisceau entier par un trait unique passant par le centre de l'échantillon.
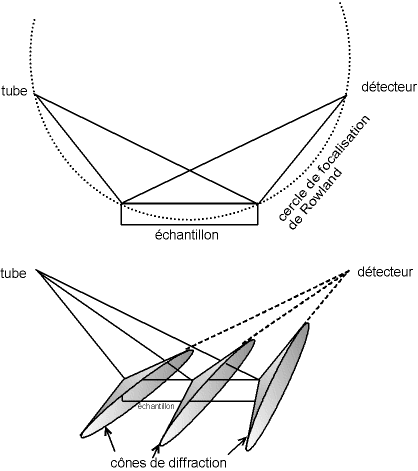
Fig. 4-9 Divergence du faisceau :
tous les cônes de diffraction passent par un même point,
en l'occurence le détecteur
Notons que le cercle de focalisation est le cercle imaginaire passant par l'échantillon, le tube et le détecteur. Il est donc différent pour chaque position angulaire. Ce cercle possède une propriété géométrique : si l'on prend n'importe quel point A de ce cerle, l'angle tube-A-détecteur est toujours le même (et si O est le centre du cercle, il vaut la moitié de l'angle tube-O-détecteur, car les deux secteurs angulaires interceptent le même arc - propriété classique de la géométrie du cercle). Ceci explique pourquoi, en faisant l'approximation que la surface de l'échantillon épouse le cercle de Rowland, si un des points de l'échantillon est en condition de bragg, tous les points le sont puisque les faisceaux ont la même déviation.
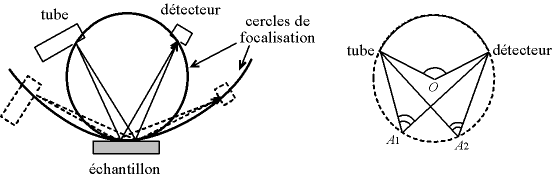
Fig. 4-10 Cercles de focalisation de Rowland :
le cercle est différent pour chaque déviation 2θ
L'effet de la largeur du faisceau est étudié plus loin, mais il peut être négligé dans un premier temps. La fenêtre du détecteur est elle aussi rectangulaire.
Lien
| début |
D'après la loi de Bragg énoncée ci-dessus, on voit qu'il y a une relation unique entre la déviation 2θ et la distance interréticulaire d (si l'on ne considère que le premier ordre de diffraction, n = 1). Un pic est présent en 2θ s'il existe, dans le cristal, des plans atomiques parallèles espacés d'une distance
d = λ/(2.sinθ).
On peut donc dire que le pic représente une distance d. Ceci présente l'avantage d'être indépendant de la longueur d'onde λ des rayons X utilisés. En effet, si l'on mesure un même échantillon avec deux longueurs d'ondes différentes, les positions en 2θ des pics seront différentes, par contre, les d seront les mêmes.
Pour cette raison, de nombreux utilisateurs affichent les diffractogrammes en (d,I). Par ailleurs, les listes de pics des signatures des produits sont toujours indiquées en (d,I).
| début |
Les rayons X d'un cône de diffraction donné (c.-à-d. pour une déviation 2θ donnée) proviennent de la diffraction de certains cristallites.
Rappelons qu'une poudre ou un échantillon massif polycristallin contiennent des domaines semblables en tous points à un monocristal ; ces domaines de cohérence sont nommés «cristallites» (dans certains domaines de la science des matériaux, on parle de «grains», mais il y a une ambiguïté avec les grains de poudre, un grain de poudre peut être constitué de plusieurs cristallites).
Pour une incidence donnée, seuls certains cristallites contribuent à un cône donné, ce sont les cristallites dont les plans (hkl) correspondant à l'angle de déviation 2θ vérifient les conditions de Bragg.
Donc, chaque cône provient de cristallites orientés de manière différente. Pour que le diffractogramme soit caractéristique des phases en présence et d'aucun autre paramètre, il faut donc que toutes les orientations cristallines soient représentées, et que les grains sous le faisceau soient suffisamment nombreux pour avoir une analyse statistique.
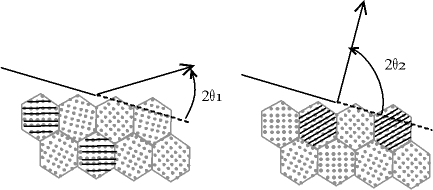
Fig. 4-11 Cristallites diffractant dans le cas d'une incidence fixe
(chambre de Debye-Scherrer)
- les plans (hkl) en condition de Bragg
sont surlignés par des traits noirs
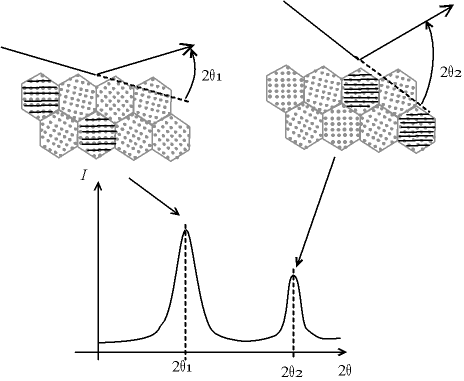
Fig. 4-12 Cristallites diffractant dans le cas
d'une incidence et d'une détection symétriques
(diffractomètre de Bragg-Brentano)
- les plans (hkl) en condition de Bragg
sont surlignés par des traits noirs
Notons que les plans (hkl) contribuant au signal sont nécessairement orthogonaux à la bissectrice entre le faisceau incident et le faisceau diffracté (bissectrice que l'on appelle aussi «vecteur de diffraction»). Dans le cas d'un diffractomètre de Bragg-Brentano, les plans diffractants sont donc parallèles à la surface de l'échantillon.