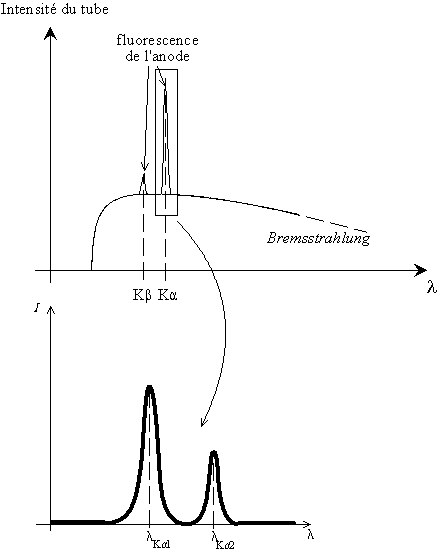
Fig. 9-1 Spectre d'émission du tube - sélection du doublet Kα1-Kα2
| Introduction | Méthodes de mesure | Recherche de phases | Principes physiques | Décalages | Surface | Largeur | Intensité | * | Biblio |
| précédent |
Nous avons vu jusqu'ici que sur un diffractogramme, la position des pics, leur surface et leur largeur étaient porteurs d'information sur le matériau. Nous allons voir ici que la forme même du pic, c.-à-d. la fonction mathématique pouvant décrire le pic, est elle aussi porteur d'information, à la fois sur l'échantillon et sur le diffractomètre. Ce profil a été étudié entres autres par Harold P. Klug et Leroy E. Alexander (1974), ainsi que Robert W. Cheary et Alan A. Coelho (Université de Sydney, Australie, 1992).
Chaque élément de la chaîne du signal a une fonction caractéristique. La forme finale du pic s'obtient en faisant le produit de convolution de toutes ces fonctions caractéristiques.
Les résultats présentés ici sont relatifs aux diffractomètres à géométrie Bragg-Brentano.
La forme du pic provient d'abord du profil d'émission du tube à rayons X. Les rayons X sont produits de la manière suivante : on bombarde une cible métallique (en général du cuivre Cu, du cobalt Co ou du molybdène Mo) avec des électrons, et les électrons, en freinant, génèrent des rayons X. C'est le rayonnement continu de freinage ou Bremsstrahlung. Les atomes de la cible sont excités par les rayons X, ils émettent un rayonnement X propre par fluorescence. C'est ce rayonnement fluorescent qui nous intéresse. La cible métallique est également appelée «anode» ou «anti-cathode».
On utilise un système monochromateur afin d'isoler une petite portion du spectre ; il peut s'agir d'un filtre absorbant ou d'un système diffractant, ou bien d'un détecteur dispersif en énergie (EDS). On ne s'intéresse qu'à la raie Kα1 de la cible.
Dans les faits, on utilise souvent le doublet Kα1-Kα2, en effet, la raie Kα2 ne gêne pas, donc inutile de dépenser de l'argent et de perdre de l'intensité en voulant l'enlever (-: mais pour certaines applications, on ne va travailler quavec la raie Kα1. On a aussi parfois une raie très petite, la raie Kβ, mais celle-ci est couramment filtrée.

Fig. 9-1 Spectre d'émission du tube -
sélection du doublet Kα1-Kα2
Ce spectre "bicéphal" va donc se décalquer. Pour les conditions de diffraction d'un plan (hkl) donné, il va se transformer par la loi de Bragg
2θ = 2.arcsin(λ/2dhkl)On va donc avoir systématiquement un pic double, mais l'écartement entre les deux pics est en arc-sinus de la demi-déviation ; donc les deux pics sont confondus aux bas angles et détachés aux grands angles.
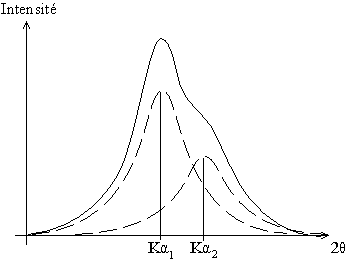
Fig. 9-2 Double pic partiellement séparé
dans une zone médiane du diffractogramme
En réalité, le doublet Kα1-Kα2 est un sextuplet (Kα1-Kα3Kα5)-(Kα2-Kα4-Kα6). Les raies Kα3, Kα4, Kα5 et Kα6 sont très faibles (raies «satellites») et sont noyées dans les pieds des raies Kα1 et Kα2 ; en apparence, on n'a donc que deux raies légèrement dissymétriques.
Chacune des ces 6 raies est représentée par une fonction lorentzienne1, c.-à-d. de la forme
f(λ) = A.[1+B.(λ-λs)2]-1où λs est la position du sommet du pic, A est une constante proportionnelle à la hauteur du pic, et B est une constante proportionnelle à l'inverse du carré de la largeur à mi-hauteur de la raie, B α 1/H2.
| début |
Le détecteur a une certaine ouverture angulaire, il n'est pas infiniment fin ; cette ouverture angulaire est limitée par une fente de réception. La largeur de la fente de réception du détecteur produit donc un élargissement des pics. Cela revient à faire un produit de convolution de la fonction des pics par une fonction porte.
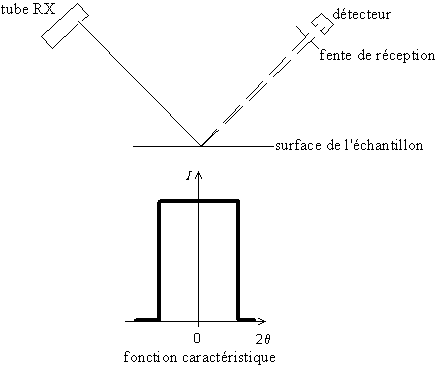
Fig. 9-3 Ouverture angulaire du détecteur
La source n'est pas ponctuelle mais a une certaine largeur. Cela produit le même effet sur le signal.
| début |
On éclaire l'échantillon avec un faisceau divergent. Pour qu'il converge parfaitement sur le détecteur, il faudrait un échantillon courbe. Comme l'échantillon est plan, on n'a qu'une divergence approchée. Ceci se traduit par une dissymétrie du pic, qui s'étale vers les faibles angles. On a une fonction caractéristique en forme de j.
Pour limiter la zone bombardée par les rayons X (et éviter d'avoir un signal ne provenant pas de l'échantillon), on limite la divergence horizontale par une fente placée entre le tube et l'échantillon, appelée «fente avant» ou «fente de divergence». Pour limiter la portion de l'échantillon "vue" par le détecteur (et éviter que celui-ci reçoive des rayons ne provenant pas de l'échantilllon), on limite la divergence horizontale par une fente placée entre l'échantillon et le détecteur, appelée «fente arrière» ou «fente anti-diffusion».
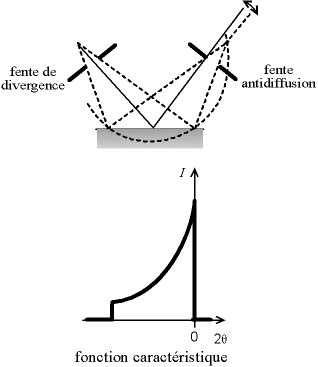
Fig. 9-4 Dissymétrie du pic
induite par la divergence horizontale du faisceau
| début |
Afin d'augmenter l'intensité, le faisceau du tube n'est pas cylindrique, il a une section rectangulaire d'une largeur d'environ 1 cm, (on éclaire une plus grande surface). Les rayons peuvent donc se croiser, l'intensité reçue n'a donc pas forcément été déviée par l'angle 2θ affiché par le goniomètre. Il s'ensuit une dissymétrie du pic vers les faibles angles. On peut limiter cet effet en untilisant un collimateur, appelé «fentes de Soller», placé avant l'échantillon : ce sont des lames de cuivre qui absorbent les rayons divergents.
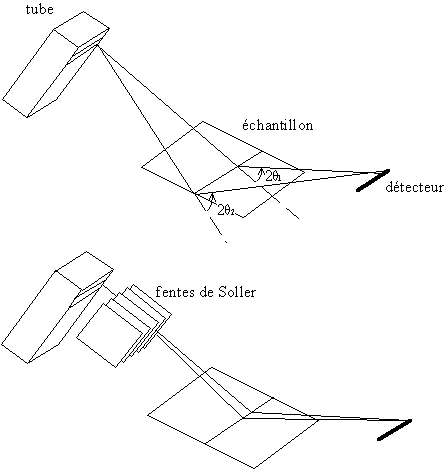
Fig. 9-5 Correction de la divergence axiale par un collimateur avant
Par ailleurs, l'ouverture du détecteur est un rectangle et non un point, toujours pour récolter le maximum d'intensité. Or, lorsqu'un faisceau ponctuel frappe l'échantillon, il produit un cône de diffraction. Donc, le détecteur va voir aussi une partie des bords du cône. Comme de plus le faisceau est à section rectangulaire, il se décompose en une multitude de faisceaux ponctuels, qui donnent une multitude de cônes. Ceci donne une dissymétrie du pic vers les faibles angles.
On limite cet effet en mettant un collimateur entre l'échantillon et le détecteur. Ces fentes de Soller "coupent" les cônes, qui deviennent donc des "tuiles".
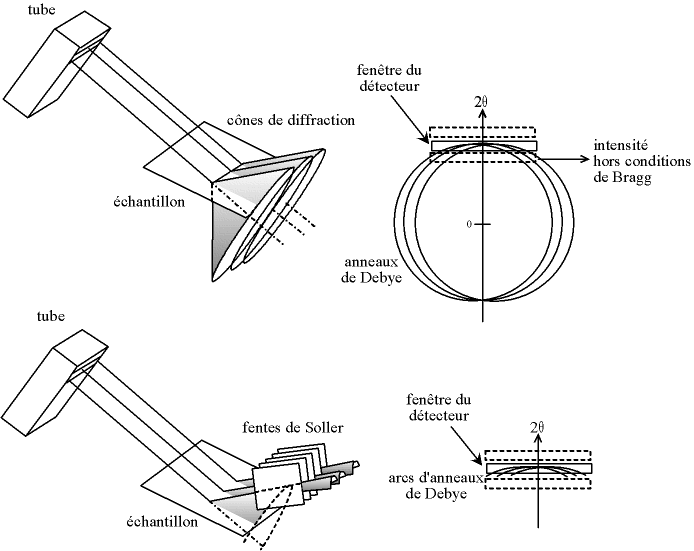
Fig. 9-6 Correction de la divergence axiale par un collimateur arrière
Cette divergence axiale, limitée par les fentes de Soller avant et arrière, a pour fonction caractéristique une courbe en j.
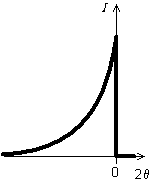
Fig. 9-7 Fonction caractéristique de la divergence axiale
| début |
Le profil instrumental est le produit de convolution du pic double généré par le spectre de la source à l'angle 2θ indiqué, par les fonctions caractéristiques décrites ci-dessus. On peut aussi estimer ce profil analytique expérimentalement en mesurant un pic sur un échantillon sans contraintes, ayant une taille de cristallites comprise entre 1 et 60 μm.
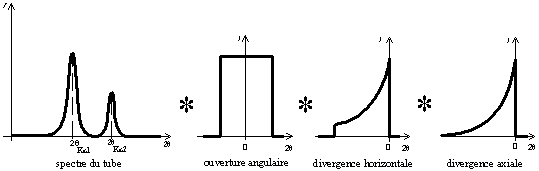
Fig. 9-8 Construction de la fonction instrumentale
par des produits de convolution
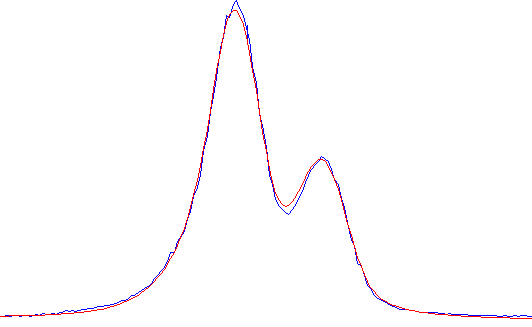
Fig. 9-9 Fonction instrumentale mesurée expérimentalement
(en bleu, échantillon de LaB6)
et simulée par produits de convolution (en rouge)
| début |
Le profil instrumental est modifié par l'échantillon. Trois paramètres entrent en jeu, dont deux ont déjà été évoqués pour la largeur du pic (les microcontraintes et la taille des cristallites).
Si un cristallite est déformé par des contraintes (forces internes), ses pics sont décalé ; si l'on a une distribution aléatoire de contraintes, on a alors plusieurs pics côte-à-côte (cf. paragraphe Microcontraintes résiduelles). Si l'on modélise la répartition des microcontraintes par une loi normale (ou loi de Gauss), le pic mesuré sera alors le produit de convolution de la fonction instrumentale par une gaussienne, c.-à-d. une fonction de la forme
f(2θ) = A.exp[-B.(2θ-2θs)2]où 2θs est la position du sommet du pic, A est une constante proportionnelle à la hauteur du pic, et B est une constante proportionnelle à l'inverse du carré de la largeur à mi-hauteur de la fonction caractéristique, B α 1/H2
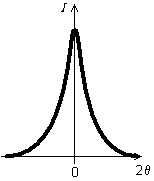
Fig. 9-10 Fonction caractéristique des microcontraintes
dans l'échantillon
Les cristallites ayant une taille limitée, le facteur de forme fait que le domaine de diffraction dans l'espace des phases n'est pas ponctuel (cf. le paragraphe Facteur de forme). Pour modéliser ceci, on fait le produit de convolution de la fonction instrumentale par une lorentzienne, c.-à-d. une fonction de la forme
f(2θ) = A.[1+B.(2θ-2θs)2]-1où 2θs est la position du sommet du pic, A est une constante proportionnelle à la hauteur du pic, et B est une constante proportionnelle à l'inverse du carré de la largeur à mi-hauteur de la fonction caractéristique, B α 1/H2
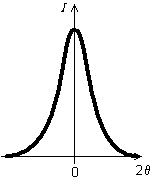
Fig. 9-11 Fonction caractéristique de la taille des cristallites
dans l'échantillon
L'échantillon absorbe plus ou moins les rayons X selon la densité et la composition chimique du matériau. Si le matériau est peu absorbant, alors les rayons X pénètrent profondément. La diffraction d'une couche profonde va donner un petit pic décalé, car c'est comme si l'on avait une erreur de hauteur (cf. paragraphe hauteur de l'échantillon).
On va donc avoir au total une superposition de pics voisins, dont la hauteur décroît lorsque l'on séloigne du sommet. Ceci provoque une dissymétrie du pics vers les faibles angles. Cet effet est négligeable sur les échantillons très absorbants.
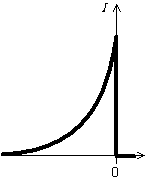
Fig. 9-12 Fonction caractéristique de l'effet d'absorption
des rayons X par l'échantillon
Le profil mesuré du pic peut s'obtenir par produit de convolution de la fonction instrumentale par les fonctions caractéristiques de l'échantillon. Connaissant le profil instrumental, et si l'on néglige l'effet d'absorption, on peut donc calculer la taille des cristallites et les microcontraintes en faisant une déconvolution du pic mesuré par une gaussienne (microcontraintes) et une lorentzienne (taille des cristallites).
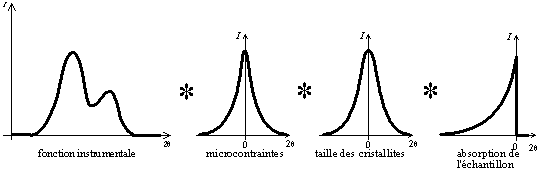
Fig. 9-13 Construction du profil du pic
par produit de convolution de la fonction instrumentale
par les fonctions caractéristiques de l'échantillon
À l'époque où l'outil informatique était moins puissant, on a développé des méthodes approchées, par exemple en utilisant la somme d'une gaussienne et d'une lorentzienne (fonction de pseudo-Voigt) plutôt qu'un produit de convolution.
Note