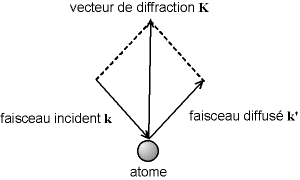
Fig. 8-1 Vecteur de diffraction
| Introduction | Méthodes de mesure | Recherche de phases | Principes physiques | Décalages | Surface | Largeur | * | Profil | Biblio |
| précédent |
lorsque l'on parle ici de «direction du détecteur», cela peut évidemment se référer à un diffractomètre Bragg-Brentano, mais également à un point de la pellicule photographique d'une chambre Debye-Scherrer.
Par ailleurs, les phénomènes de diffraction sont exactement les mêmes dans un diffractomètre Bragg-Brentano et dans une chambre de Debye-Scherrer. Les deux ne sont pas à opposer. Par contre, il est vrai que la vision que l'on en a diffère, car dans le premier cas on ne s'intéresse qu'à une seule direction de diffusion (celle du détecteur), dans le deuxième on s'intéresse aux cônes de diffraction. mais c'est notre vision qui change, pas les phénomènes...
Les rayons X sont des ondes électromagnétiques, c.-à-d. une variation périodique des champs électrique et magnétique qui se déplace. C'est donc une fonction du temps t et de la position dans l'espace r (c'est un vecteur). Comme toutes les ondes, on peut les décrire avec un fonction d'onde ψ(t,r)(1)
ψ(t,r) = A.exp[i.(ω.t+k.r)+α]où
La diffusion Rayleigh se fait dans toutes les directions, en conservant la même longueur d'onde (diffusion élastique), l'onde diffusée par un atome jpeut donc s'écrire :
ψ'(t,r) = A.fj.exp[i.(ω.t+k'.r+αj)]où fj est le facteur de diffusion atomique qui dépend de la nature chimique de l'atome, et αj est la phase qui dépend de la position de l'atome par rapport à la source de rayons X. k' est le vecteur d'onde de l'onde diffusée, qui a la même norme que k ; si l'on a un détecteur ponctuel, on ne s'intéresse qu'à l'onde entrant dans le détecteur, la direction de k' est donc l'axe échantillon-détecteur.
Si l'on prend un point de référence O, pour lequel la phase est αO, on a alors
αi = αO+K.rjK = k'-k étant le vecteur de diffraction, rj étant le vecteur position entre O et l'atome j. On peut fixer arbitrairement αO = 0.

Fig. 8-1 Vecteur de diffraction
Pour avoir l'intensité diffractée dans une direction k' par un cristallite, il suffit de faire la somme des ondes diffusées par tous les atomes j du cristallite.
Certains auteurs utilisent k = 1/λ et écrivent ψ=A.exp[i.(ω.t+2π.k.r+α)].
| début |
Considérons les atomes présents dans une seule maille cristalline. La somme des ondes diffractées par les atomes de cette maille vaut
ψ'1 = A.exp[i.(ω.t+k'.r)].F(K)avec
F(K) = Σj fj.exp(i.K.rj)F est appelé «facteur de structure», car il est caractéristique de la structure cristallographique.
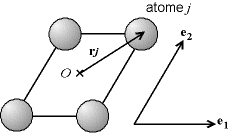
Fig. 8-2 Maille cristalline et facteur de structure
Pour que F soit maximal (c'est à dire que l'on ait un pic), il faut que les rayons diffusés soient en phase, donc que leur déphasage soit le même à 2π radians près, soit K.rj = K.rl [2π] pour tous les atomes de la maille deux à deux. Si (e1,e3,e3) sont les vecteurs de base de la maille (c.-à-d. les vecteurs des arrêtes non coplanaires), les positions des atomes s'écrivent
rj = x.e1 + y.e2 + z.e3x, y et z sont des réels positifs inférieurs à 1. De ceci, on déduit la condition de diffraction de Laue : il y a un maximum d'intensité si K est une combinaison linéaire entière des vecteurs de la base conjuguée (e*1,e*3,e*3) définie par
e*1 = 2π.e2ˆe3/VV = e1.(e2ˆe3) étant le volume d'une maille élémentaire ; on a ei.e*i = 2π, et ei.e*j = 0 si i ≠ j.
e*2 = 2π.e3ˆe1/V
e*1 = 2π.e1ˆe2/V
On peut donc écrire K = h.e*1+k.e*2+l.e*3, h, k et l étant des entiers. On peut ainsi indicer les vecteurs de diffraction donnant un maximum d'intensité par ces indices et écrire Khkl. On a donc un pic de diffraction si le détecteur se trouve dans une direction k' = k+Khkl. Le facteur de structure est alors noté Fhkl.
Lorsque K vaut Khkl (pour h, k et l donnés), cela signifie que les rayons diffusés dans la direction du détecteur par tous les atomes d'un même plan cristallographique (hkl) dans le monocristal ont la même phase, on peut donc dire que le pic de diffraction est généré par ce plan (hkl) ; on retrouve ainsi la loi de Bragg.
Pour être rigoureux, il faudrait parler du «facteur de structure lorsque les rayons diffusés par les atomes des plans (hkl) dans la direction du détecteur sont en phase», mais par abus de langage, on parle du «facteur de structure du plan (hkl)».
Prenons un espace à trois dimensions, avec la base vectorielle (e*1,e*3,e*3), et traçons-y le vecteur de diffraction K (partant de l'origine) - rappel : K est imposé par les positions du tube et du détecteur par rapport au cristallite. Il n'y a diffraction que si l'extrémité de K est sur un point dont les coordonnées dans le repère sont entières. On a ainsi, dans cet espace, un réseau en 3D de points de coordonnées entières correspondant aux conditions de diffraction.
Les vecteurs du réseau réciproque sont parallèles aux vecteurs de la base cristalline, mais les rapports des longueurs sont inversés : si e3 est le vecteur le plus long de l'espace direct, e*3 sera le vecteur le plus court du réseau réciproque.
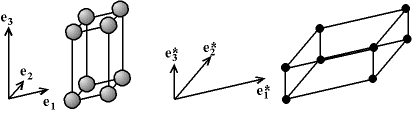
Fig. 8-3 Comparaison entre les réseaux direct et réciproque
Lorsque l'extrémité du vecteur K est sur le point de coordonnées (h,k,l), les rayons X diffusés dans la direction du détecteur par les atomes des plans (hkl) sont en phase, on peut donc dire que ce point représente le plan (hkl), et que la position dans cet espace représente la phase des rayons X.
On parle donc d'«espace des phases» ; le réseau de points dans cet espace est appelé «réseau réciproque».
Considérons un cristallite dans l'échantillon ; traçons son réseau réciproque. Avec un diffractomètre de Bragg-Brentano, en cours de mesure, le vecteur de diffraction K reste sur la même droite, garde la même direction, seule sa longueur varie.
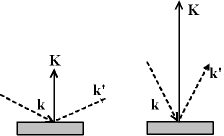
Fig. 8-4 Évolution du vecteur de diffraction K
au cours de la mesure
Le cristallite contribue au signal difracté si l'extrémité du vecteur K coïncide avec un noeud du réseau réciproque.
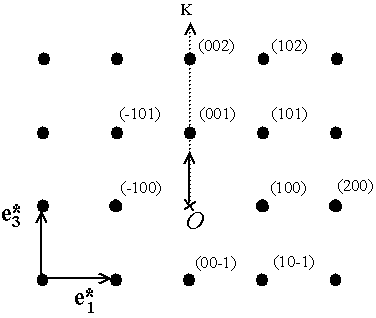
Fig. 8-5 Conditions de diffraction d'un cristallite donné
dans l'espace des phases
pour un diffractomètre Bragg-Brentano
Si l'on considère un cristallite orienté différemment, son réseau est identique sauf qu'il est tourné dans l'espace. Si l'on représente tous lieux de diffraction possible, c.-à-d. tous les noeuds des réseaux réciproques de tous les cristallites, on obtient des sphères concentriques. Il y aura donc diffraction chaque fois que l'extrémité de K se trouve sur une de ces sphère des noeuds.
Si l'on a un phénomène d'orientation préférentielle, alors les sphères ne seront pas complètes.
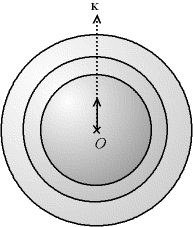
Fig. 8-6 Conditions de diffraction d'un échantillon polycristallin
dans l'espace des phases
Considérons maintenant une chambre de Debye-Scherrer. Le vecteur incident k est fixe. Les vecteurs diffractés possibles sont des vecteurs k' ayant la même longueur 2π/λ, et orientés dans tous les sens. Comme K = k'-k, si l'on trace tous les K obtenus avec tous les k' possibles, on obtient une sphère de rayon 2π/λ, centrée sur l'origine de k, l'extrémité de k étant O. Cette sphère porte le nom de «sphère d'Ewald». Elle passe par O.
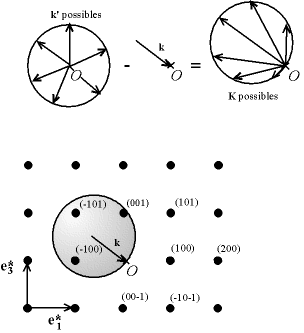
Fig. 8-7 Sphère d'Ewald :
conditions de diffraction d'un cristallite donné
dans l'espace des phases
pour une chambre Debye-Scherrer
Pour avoir les conditions de diffraction de tout l'échantillon, il suffit de faire tourner le réseau réciproque autour de O comme précédemment ; les directions de diffraction correspondent aux vecteurs de diffraction K dont l'extrémité se trouve à l'intersection de la sphère d'Ewald avec les sphères composées des noeuds des réseaux réciproques de tous les cristallites. Une telle intersection est un cercle (représenté en perspective sur la figure 8-8, donc comme un ellipse) ; le lieu des extrémités des vecteurs diffractés k' = k+K est aussi un cercle, on obtient donc bien des cônes de diffraction.
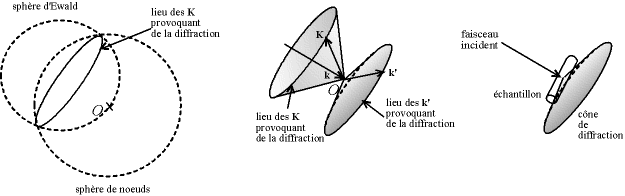
Fig. 8-8 Génération des cônes de diffraction
Si l'on applique ceci à la vision Bragg-Brentano, on voit que le vecteur K normal à la surface de l'échantillon est l'intersection de la sphère d'Ewald avec l'axe des z, l'axe (O,e*3). Lorsque la sphère d'Ewald tourne, la cote de cette intersection évolue, ce qui fait varier la longueur de K.
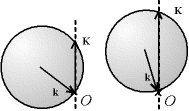
Fig. 8-9 Sphère d'Ewald
et vecteur de diffraction dans une géométrie Bragg-Brentano
- comparer avec la figure 8-4
Pour appliquer les conditions d'Ewald de diffraction sur une poudre (ensemble de cristallites ayant toutes les orientations possibles), on peut de manière symétrique considérer que l'on a :
Cette enveloppe porte le nom de «sphère de résolution». On voit immédiatement que plus la longueur d'onde est petite, plus cette sphère sera grande, donc plus on pourra voir de pics sur le diffractogramme. Plus un point est loin de l'origine O, plus le plan (hkl) qu'il représente a une distance interréticulaire dhkl petite. Donc en diminuant la longueur d'onde, on augmente la résolution de l'appareil puisque l'on "voit" des distances plus petites. On voit aussi que si la longueur d'onde est trop grande, la sphère de résolution est trop petite, donc on n'obtient aucun pic de diffraction.
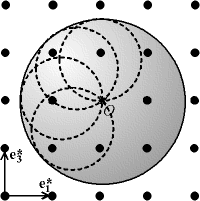
Fig. 8-10 Sphère de résolution
Note :
si l'on utilise la convention k = 1/λ,
alors le rayon de la sphère d'Ewald vaut 1/λ
et celui de la sphère de résolution vaut 2/λ.
| début |
Nous avons ci-dessus travaillé sur les rayons diffusés par les atomes d'une même maille. Un monocristal est un empilement de ces mailles, donc pour avoir la fonction de l'onde totale diffractée par le cristal, il faut sommer les fonctions d'onde ψ1 pour chaque maille. La maille j est décalée d'une translation uj = a.e1+b.e2+c.e3, a, b et c étant des entiers.
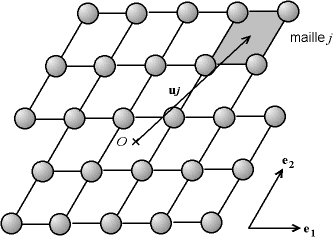
Fig. 8-11 Contribution de toutes les mailles,
définition du facteur de forme
Si ψ'1 O est la fonction d'onde diffractée par la maille située à l'origine, et ψ'1 j celle diffractée par la maille j, alors
ψ'1 j = ψ'1 O.exp(i.K.uj)
L'intensité diffractée totale est donc
ψ'2 = Σj ψ'1 jsoit
ψ'2 = A.exp[i.(ω.t+k'.r)].F(K).LKavec
LK = Σj exp(i.K.uj)LK dépend de la forme du cristal et de ses dimensions, il porte donc le nom de «facteur de forme».
Lorsque le vecteur de diffraction vaut Khkl, on note le facteur de forme Lhkl ; pour être rigoureux, il faudrait parler du «facteur de forme lorsque les rayons diffusés par les atomes des plans (hkl) dans la direction du détecteur sont en phase», mais par abus de langage, on parle du «facteur de forme du plan (hkl)».
Ce facteur de forme joue sur l'élargissement des raies (cf. paragraphe Taille des cristallites). Si le cristal a des dimensions infinies, alors les conditions de diffraction s'arrêtent dès que l'extrémité de K a quitté le noeud du réseau réciproque. Si le cristal a des dimensions finies, on a une petite sphère autour du noeud, tant que l'extrémité de K est dans cette sphère, on est en condition de diffraction.
Si l'on travaille en surface de pic du diffractogramme, on intègre ce facteur de forme et l'on trouve 1, celui-ci ne joue donc pas de rôle dans l'intensité intégrale.
Les cristallites ne sont en fait pas sphériques, ce sont des polyèdres (les joints de grain sont plans car ils suivent les plans cristallins denses, ceci permet de minimiser l'énergie d'interface) ; mais comme les faces des divers polyèdres ne sont pas parallèles, on obtient globalement des zones de diffraction sphériques lorsque l'on prend tous les cristallites de même orientation. Si maintenant les grains sont plutôt applatis (galettes), les zones de diffraction seront alors plutôt des aiguilles dont l'axe est perpendiculaire au plan des galettes.
| début |
L'intensité intégrale Ihkl, c.-à-d. la surface d'un pic de diffraction, correspond à l'énergie diffractée par le plan (hkl), donc elle est proportionnelle au carré de la norme de la fonction d'onde ψ'2. Il faut ajouter à ceci un facteur de polarisation P = (1+cos2(2θ))/2, et le facteur de Lorentz L = 1/sin(2θ), qui correspond au temps durant lequel le plan (hkl) est en condition de diffraction (si 2θ varie à vitesse constante).
L'intensité intégrale vaut :
Ihkl = I0.|Fhkl|2.L.P.exp[-B.sin2(θ)/λ2]où I0 est l'intensité de référence, qui dépend de l'intensité incidente, de la quantité de produit (volume diffractant) et du rendement des détecteurs, et B est une constante appelée «facteur de Debye» ; le terme exponentiel à la fin provient de l'agitation thermique des atomes. Si plusieurs pics sont au même endroit, il faut additionner les intensités des pics. Lorsque les indices de Miller (hkl) des plans dont les pics sont au même endroit sont semblables, on parle de «multiplicité» des pics. Par exemple, pour les cristaux de structure cubique, les pics des plans (100), (010), (001), (-100), (0-10) et (00-1) sont superposés, on dit que le pic (100) a une multiplicité de 6 (ces 6 plans forment une même famille notée {100}).
L et P dépendent de 2θ, mais comme les deux fonctions sont toujours associées, on note cela comme une seule fonction LP(2θ). Les valeurs de LP sont tabulées.
Notes